A normalization model of multisensory integration
- PMID: 21552274
- PMCID: PMC3102778
- DOI: 10.1038/nn.2815
A normalization model of multisensory integration
Abstract
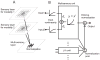
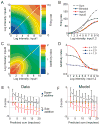
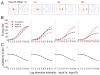
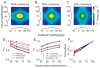
Responses of neurons that integrate multiple sensory inputs are traditionally characterized in terms of a set of empirical principles. However, a simple computational framework that accounts for these empirical features of multisensory integration has not been established. We propose that divisive normalization, acting at the stage of multisensory integration, can account for many of the empirical principles of multisensory integration shown by single neurons, such as the principle of inverse effectiveness and the spatial principle. This model, which uses a simple functional operation (normalization) for which there is considerable experimental support, also accounts for the recent observation that the mathematical rule by which multisensory neurons combine their inputs changes with cue reliability. The normalization model, which makes a strong testable prediction regarding cross-modal suppression, may therefore provide a simple unifying computational account of the important features of multisensory integration by neurons.
Figures


Comment in
-
Normalizing relations between the senses.Nat Neurosci. 2011 Jun;14(6):672-3. doi: 10.1038/nn.2850. Nat Neurosci. 2011. PMID: 21613993 No abstract available.
References
-
- Alais D, Burr D. The ventriloquist effect results from near-optimal bimodal integration. Curr Biol. 2004;14:257–262. - PubMed
-
- Ernst MO, Banks MS. Humans integrate visual and haptic information in a statistically optimal fashion. Nature. 2002;415:429–433. - PubMed
-
- Stein BE, Stanford TR. Multisensory integration: current issues from the perspective of the single neuron. Nat Rev Neurosci. 2008;9:255–266. - PubMed
-
- Meredith MA, Stein BE. Visual, auditory, and somatosensory convergence on cells in superior colliculus results in multisensory integration. J Neurophysiol. 1986;56:640–662. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

