Behavior and neural basis of near-optimal visual search
- PMID: 21552276
- PMCID: PMC3713779
- DOI: 10.1038/nn.2814
Behavior and neural basis of near-optimal visual search
Abstract
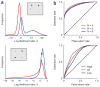
The ability to search efficiently for a target in a cluttered environment is one of the most remarkable functions of the nervous system. This task is difficult under natural circumstances, as the reliability of sensory information can vary greatly across space and time and is typically a priori unknown to the observer. In contrast, visual-search experiments commonly use stimuli of equal and known reliability. In a target detection task, we randomly assigned high or low reliability to each item on a trial-by-trial basis. An optimal observer would weight the observations by their trial-to-trial reliability and combine them using a specific nonlinear integration rule. We found that humans were near-optimal, regardless of whether distractors were homogeneous or heterogeneous and whether reliability was manipulated through contrast or shape. We present a neural-network implementation of near-optimal visual search based on probabilistic population coding. The network matched human performance.
Conflict of interest statement
The authors declare no competing financial interests.
Figures




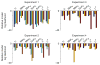
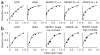
References
-
- Palmer J, Ames CT, Lindsey DT. Measuring the effect of attention on simple visual search. J Exp Psychol Hum Percept Perform. 1993;19:108–130. - PubMed
-
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognit Psychol. 1980;12:97–136. - PubMed
-
- Shaw ML. Identifying attentional and decision-making components in information processing. In: Nickerson RS, editor. Attention and Performance. Erlbaum; Hillsdale, New Jersey: 1980. pp. 277–296.
-
- Teichner WH, Krebs MJ. Visual search for simple targets. Psychol Bull. 1974;81:15–28. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

