Mechanical control of cation channels in the myogenic response
- PMID: 21572020
- PMCID: PMC3154678
- DOI: 10.1152/ajpheart.00131.2011
Mechanical control of cation channels in the myogenic response
Abstract
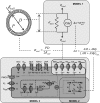
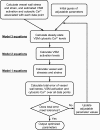
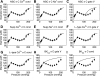
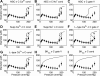
Microcirculatory vessel response to changes in pressure, known as the myogenic response, is a key component of a tissue's ability to regulate blood flow. Experimental studies have not clearly elucidated the mechanical signal in the vessel wall governing steady-state reduction in vessel diameter upon an increase in intraluminal pressure. In this study, a multiscale computational model is constructed from established models of vessel wall mechanics, vascular smooth muscle (VSM) force generation, and VSM Ca(2+) handling and electrophysiology to compare the plausibility of vessel wall stress or strain as an effective mechanical signal controlling steady-state vascular contraction in the myogenic response. It is shown that, at the scale of a resistance vessel, wall stress, and not stretch (strain), is the likely physiological signal controlling the steady-state myogenic response. The model is then used to test nine candidate VSM stress-controlled channel variants by fitting two separate sets of steady-state myogenic response data. The channel variants include nonselective cation (NSC), supplementary Ca(2+) and Na(+), L-type Ca(2+), and large conductance Ca(2+)-activated K(+) channels. The nine variants are tested in turn, and model fits suggest that stress control of Ca(2+) or Na(+) influx through NSC, supplementary Ca(2+) or Na(+), or L-type Ca(2+) channels is sufficient to produce observed steady-state diameter changes with pressure. However, simulations of steady-state VSM membrane potential, cytosolic Ca(2+), and Na(+) with pressure show only that Na(+) influx through NSC channel also generates known trends with increasing pressure, indicating that stress-controlled Na(+) influx through NSC is sufficient to generate the myogenic response.
Figures

References
-
- Baek EB, Jin C, Park SJ, Park KS, Yoo HY, Jeon JH, Earm YE, Kim SJ. Differential recruitment of mechanisms for myogenic responses according to luminal pressure and arterial types. Pflügers Arch 460: 19–29, 2010 - PubMed
-
- Bund SJ. Spontaneously hypertensive rat resistance artery structure related to myogenic and mechanical properties. Clin Sci (Lond) 101: 385–393, 2001 - PubMed
-
- Carlson BE, Secomb TW. A theoretical model for the myogenic response based on the length-tension characteristics of vascular smooth muscle. Microcirculation 12: 327–338, 2005 - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

