Bayesian inference underlies the contraction bias in delayed comparison tasks
- PMID: 21589867
- PMCID: PMC3093393
- DOI: 10.1371/journal.pone.0019551
Bayesian inference underlies the contraction bias in delayed comparison tasks
Abstract
Delayed comparison tasks are widely used in the study of working memory and perception in psychology and neuroscience. It has long been known, however, that decisions in these tasks are biased. When the two stimuli in a delayed comparison trial are small in magnitude, subjects tend to report that the first stimulus is larger than the second stimulus. In contrast, subjects tend to report that the second stimulus is larger than the first when the stimuli are relatively large. Here we study the computational principles underlying this bias, also known as the contraction bias. We propose that the contraction bias results from a Bayesian computation in which a noisy representation of a magnitude is combined with a-priori information about the distribution of magnitudes to optimize performance. We test our hypothesis on choice behavior in a visual delayed comparison experiment by studying the effect of (i) changing the prior distribution and (ii) changing the uncertainty in the memorized stimulus. We show that choice behavior in both manipulations is consistent with the performance of an observer who uses a Bayesian inference in order to improve performance. Moreover, our results suggest that the contraction bias arises during memory retrieval/decision making and not during memory encoding. These results support the notion that the contraction bias illusion can be understood as resulting from optimality considerations.
Conflict of interest statement
Figures
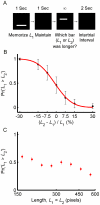
 and the ordinate corresponds to the fraction of trials in which subjects chose L
1 as longer than L
2. Error bars depict standard error of the mean (SEM). Line is a least-square fit of an error function:
and the ordinate corresponds to the fraction of trials in which subjects chose L
1 as longer than L
2. Error bars depict standard error of the mean (SEM). Line is a least-square fit of an error function:  where
where  and
and  . C, Average response curve of 9 subjects. Fraction of times in which subjects reported ‘L
1>L
2’ on the impossible trials are plotted as a function of bar length. Subjects overestimated the magnitude of the memorized L
1 bar when it was relatively small and underestimated L
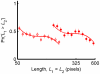
1 when it was relatively long, consistent with the contraction bias. Each data point corresponds to 21 impossible trials per subject. Error bars depict SEM.
. C, Average response curve of 9 subjects. Fraction of times in which subjects reported ‘L
1>L
2’ on the impossible trials are plotted as a function of bar length. Subjects overestimated the magnitude of the memorized L
1 bar when it was relatively small and underestimated L
1 when it was relatively long, consistent with the contraction bias. Each data point corresponds to 21 impossible trials per subject. Error bars depict SEM.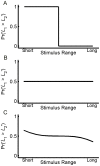
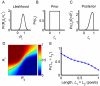
 . B, The prior distribution of bar lengths. C, The posterior distribution of Li given a particular measurement (here Ri = 0.85), calculated using Bayes' rule. D, The probability that L
1>L
2 for different values of R
1 and R
2, computed using the posteriors. The black line corresponds to the values of R
1 and R
2 such that Pr(L
1>L
2|R
1,R
2) = 0.5 (here,
. B, The prior distribution of bar lengths. C, The posterior distribution of Li given a particular measurement (here Ri = 0.85), calculated using Bayes' rule. D, The probability that L
1>L
2 for different values of R
1 and R
2, computed using the posteriors. The black line corresponds to the values of R
1 and R
2 such that Pr(L
1>L
2|R
1,R
2) = 0.5 (here,  and
and  ). E, Response curve of the model on the impossible trials in which L
1 = L
2.
). E, Response curve of the model on the impossible trials in which L
1 = L
2.References
-
- Hollingworth HL. The Central Tendency of Judgment. The Journal of Philosophy, Psychology and Scientific Methods. 1910;7:461–469.
-
- Berliner JE, Durlach NI, Braida LD. Intensity perception. VII. Further data on roving-level discrimination and the resolution and bias edge effects. The Journal of the Acoustical Society of America. 1977;61:1577–1585. - PubMed
-
- Hellstrom A. The time-order error and its relatives: Mirrors of cognitive processes in comparing. Psychological Bulletin. 1985;97:35–61.
-
- Marks LE. Contextual processing of multidimensional and unidimensional auditory stimuli. Journal of experimental psychology: Human perception and performance. 1993;19:227–249. - PubMed
-
- Wilken P, Ma WJ. A detection theory account of change detection. J Vis. 2004;4:1120–1135. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

