Acoustic signatures of sound source-tract coupling
- PMID: 21599213
- PMCID: PMC3909991
- DOI: 10.1103/PhysRevE.83.041920
Acoustic signatures of sound source-tract coupling
Abstract
Birdsong is a complex behavior, which results from the interaction between a nervous system and a biomechanical peripheral device. While much has been learned about how complex sounds are generated in the vocal organ, little has been learned about the signature on the vocalizations of the nonlinear effects introduced by the acoustic interactions between a sound source and the vocal tract. The variety of morphologies among bird species makes birdsong a most suitable model to study phenomena associated to the production of complex vocalizations. Inspired by the sound production mechanisms of songbirds, in this work we study a mathematical model of a vocal organ, in which a simple sound source interacts with a tract, leading to a delay differential equation. We explore the system numerically, and by taking it to the weakly nonlinear limit, we are able to examine its periodic solutions analytically. By these means we are able to explore the dynamics of oscillatory solutions of a sound source-tract coupled system, which are qualitatively different from those of a sound source-filter model of a vocal organ. Nonlinear features of the solutions are proposed as the underlying mechanisms of observed phenomena in birdsong, such as unilaterally produced "frequency jumps," enhancement of resonances, and the shift of the fundamental frequency observed in heliox experiments.
©2011 American Physical Society
Figures





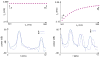
References
-
- Zeigler P, Marler P. Neuroscience of Birdsong. Cambridge University Press; Cambridge, MA: 2004.
-
- Doupe AJ, Kuhl PK. Annu Rev Neurosci. 1999;22:567. - PubMed
-
- Goller F, Cooper BG. Ann NY Acad Sci. 2004;1016:130. - PubMed
-
- Mindlin G, Laje R. The Physics of Birdsong. Springer; Berlin: 2005.
-
- Larsen ON, Goller F. Proc Biol Sci. 1999;266:1609.
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
