Modeling routes of chronic wasting disease transmission: environmental prion persistence promotes deer population decline and extinction
- PMID: 21603638
- PMCID: PMC3094393
- DOI: 10.1371/journal.pone.0019896
Modeling routes of chronic wasting disease transmission: environmental prion persistence promotes deer population decline and extinction
Abstract
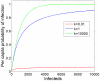
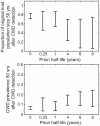
Chronic wasting disease (CWD) is a fatal disease of deer, elk, and moose transmitted through direct, animal-to-animal contact, and indirectly, via environmental contamination. Considerable attention has been paid to modeling direct transmission, but despite the fact that CWD prions can remain infectious in the environment for years, relatively little information exists about the potential effects of indirect transmission on CWD dynamics. In the present study, we use simulation models to demonstrate how indirect transmission and the duration of environmental prion persistence may affect epidemics of CWD and populations of North American deer. Existing data from Colorado, Wyoming, and Wisconsin's CWD epidemics were used to define plausible short-term outcomes and associated parameter spaces. Resulting long-term outcomes range from relatively low disease prevalence and limited host-population decline to host-population collapse and extinction. Our models suggest that disease prevalence and the severity of population decline is driven by the duration that prions remain infectious in the environment. Despite relatively low epidemic growth rates, the basic reproductive number, R(0), may be much larger than expected under the direct-transmission paradigm because the infectious period can vastly exceed the host's life span. High prion persistence is expected to lead to an increasing environmental pool of prions during the early phases (i.e. approximately during the first 50 years) of the epidemic. As a consequence, over this period of time, disease dynamics will become more heavily influenced by indirect transmission, which may explain some of the observed regional differences in age and sex-specific disease patterns. This suggests management interventions, such as culling or vaccination, will become increasingly less effective as CWD epidemics progress.
Conflict of interest statement
Figures


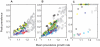



References
-
- Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. New York: Oxford University Press.; 1991. 757
-
- Sauvage F, Langlais M, Yoccoz NG, Pontier D. Modelling hantavirus in fluctuating populations of bank voles: the role of indirect transmission on virus persistence. Journal of Animal Ecology. 2003;72:1–13.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Research Materials

