Silicon-Neuron Design: A Dynamical Systems Approach

Abstract

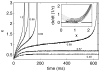
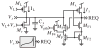
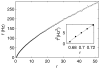
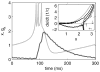
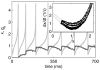
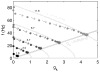
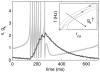
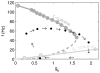
We present an approach to design spiking silicon neurons based on dynamical systems theory. Dynamical systems theory aids in choosing the appropriate level of abstraction, prescribing a neuron model with the desired dynamics while maintaining simplicity. Further, we provide a procedure to transform the prescribed equations into subthreshold current-mode circuits. We present a circuit design example, a positive-feedback integrate-and-fire neuron, fabricated in 0.25 μm CMOS. We analyze and characterize the circuit, and demonstrate that it can be configured to exhibit desired behaviors, including spike-frequency adaptation and two forms of bursting.

Fig. 1

Measured silicon neuron membrane traces (x, normalized) rise like a resistor-capacitor circuit, with a positive feedback spike for several step-input current levels (r=0.48, 0.57, 0.69, 0.82, 0.98, and 1.2). Below a threshold input, the neuron reaches a steady state at which the input and positive feedback are insufficient to overpower the leak. Above threshold, larger inputs enable the positive feedback to overcome the leak more quickly, resulting in a shorter time to spike. Inset The neuron’s phase plot shows ẋ versus x (black), fit with a cubic (gray). The neuron has two fixed points (circles) when its input is small, r < 2/3, one stable (filled) and one unstable (open). As r increases above 2/3, the fixed points merge and destroy each other, undergoing a saddle-node bifurcation, the transition from resting to spiking. Phase plot traces filtered by a 5 ms halfwidth gaussian.

Fig. 2

The neuron circuit comprises a capacitor C_x, driven by three currents: an input (M_r), a leak (M_L), and positive feedback (M_F1–5). When the input and positive feedback currents drive V_x low enough, REQ transitions from low to high, signaling a spike.

Fig. 3

The silicon neuron responds sublinearly to current above a threshold (dots). See text for fit equation. Inset f² is fit (gray line) versus the input to find and normalize to the threshold r = 2/3.

Fig. 4

The neuron expresses frequency bistability when reset to 1.7. Initially, when the input is low, r = 0.36, the neuron is silent, but when it increases to 0.70 then, drops back to 0.36, the neuron spikes at 22 Hz. Inset The neuron trajectory (black) follows the fits for r = 0.36, 0.70 (gray). When it is reset above the unstable point (open circle) for r = 0.36, the neuron spikes; otherwise it sits at the stable point (filled circle). Phase plot traces filtered by a 5 ms halfwidth gaussian.

Fig. 5

In square-wave bursting, as g_k decays the burst begins, x spikes rapidly until g_k overcomes the positive feedback. Inset The neuron rests at its stable point (closed circle), which becomes destabilized when the ẋ versus x curve rises as g_k decays, starting a burst (arrows). During the burst, the ẋ versus x curve drops as g_k rises, eventually pushing the unstable point (open circle) above x_res, which terminates the burst. Phase plot and g_k traces filtered by a 5 ms halfwidth gaussian.

Fig. 6

The ion-channel population circuit consists of two modules, one implements the pulse-like spike response, p(t) (M_p1,2 and C_p), and the other implements the first-order dynamics, V_ch (M_ch1–3 and C_ch). V_ch generates the output current, I_ch, when it is applied to the gate of an output transistor M_out.

Fig. 7

To implement adapting and bursting the neuron circuit is augmented with two ion-channel population circuits, realizing g_k (M_k) and r_ca (M_ca), and a reset circuit (M_res).

Fig. 8

In square-wave bursting, x and g_k follow a trajectory (black) in which x moves towards either a stable equilibrium or a spiking limit cycle. Initially for low g_k (below 0.22), x enters the spiking limit cycle (light gray shading). As g_k increases (between 0.22 and 1.22), x remains in its spiking limit cycle, even though a stable point and an unstable point have appeared (solid and dashed lines). Once g_k exceeds 1.22, the limit cycle becomes unstable (dark gray shading); x drops to its only stable point, until g_k decays below 0.22, repeating the cycle. Traces filtered by a 5 ms halfwidth gaussian; dots are 5 ms apart.

Fig. 9

In spike-frequency adaptation, as g_k (dark gray) increases x’s (light gray) spike frequency decreases. Inset g_k decreases frequency by decreasing ẋ (black) towards zero, slowing spiking. Fits (gray) are a guide for the eye. Phase plot and g_k traces filtered by 10 and 5 ms halfwidth gaussians, respectively.

Fig. 10

In spike-frequency adaptation, f starts high but decreases as g_k increases (arrows), following the f-nullcline (light gray) until it crosses the g_k nullcline, reaching a stable equilibrium. Each dot corresponds to one interspike interval’s instantaneous f and mean g_k. g_k values filtered by a 5 ms halfwidth gaussian.

Fig. 11

In parabolic bursting, as g_k (dark gray) decays the burst begins, x (light) spikes faster then slower until the burst ends. Inset g_k shifts the conceptual f(r_ca) curve. For medium g_k (middle curve), two stable points coexist (filled circles), one at a high frequency and one at a low, with an unstable point in between (open circle). For low g_k (top curve), the low stable point collides with the unstable point, leaving only the high stable point, initiating spiking. For high g_k (bottom curve), the high stable point collides with the unstable point, leaving only the low stable point, terminating spiking. g_k filtered by a 5 ms halfwidth gaussian.

Fig. 12

In parabolic bursting, f and g_k follow a trajectory (black) in which both move towards stable portions of their respective nullclines (dark and light gray). Each dot corresponds to one interspike interval’s instantaneous f and mean g_k. g_k values filtered by a 5 ms halfwidth gaussian.