Attracting dynamics of frontal cortex ensembles during memory-guided decision-making

Abstract

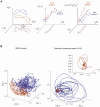
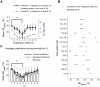
A common theoretical view is that attractor-like properties of neuronal dynamics underlie cognitive processing. However, although often proposed theoretically, direct experimental support for the convergence of neural activity to stable population patterns as a signature of attracting states has been sparse so far, especially in higher cortical areas. Combining state space reconstruction theorems and statistical learning techniques, we were able to resolve details of anterior cingulate cortex (ACC) multiple single-unit activity (MSUA) ensemble dynamics during a higher cognitive task which were not accessible previously. The approach worked by constructing high-dimensional state spaces from delays of the original single-unit firing rate variables and the interactions among them, which were then statistically analyzed using kernel methods. We observed cognitive-epoch-specific neural ensemble states in ACC which were stable across many trials (in the sense of being predictive) and depended on behavioral performance. More interestingly, attracting properties of these cognitively defined ensemble states became apparent in high-dimensional expansions of the MSUA spaces due to a proper unfolding of the neural activity flow, with properties common across different animals. These results therefore suggest that ACC networks may process different subcomponents of higher cognitive tasks by transiting among different attracting states.

Figure 1. Unfolding trajectories by expanding state space dimensionality.

A. Left: In this schema, the two-dimensional reconstruction of a three-dimensional dynamical system in the plane (x ₁, x ₂) causes two trajectories to intersect with themselves and with each other multiple times (as indicated by the dots). At each of these intersection points, the flow of the system (the change of activity in time) is not uniquely defined as indicated by the arrows and question marks. However, such a unique determination of flow would be important for assessing, e.g., the convergence of trajectories. Center: A potential solution: While it may not be possible to discriminate between two trajectories within a two-dimensional plane spanned by the firing rates of two neurons, (ν₁(t), ν₂(t)), adding a third axis containing an appropriate time delay for one of the units permits to fully disentangle the two trajectories. Right: High-order products of delayed firing rates, e.g. ν² ₁(t-τ₁) ν³ ₂(t-τ₂), further amplify the trajectory separation already achieved through the delays. Thus, dimensions missing from the original space can be substituted by new axes formed from the measured variables. B. Three-dimensional projections obtained by Principal Components Analysis (PCA) for a single trial (#1) of rat #1 (see text). Brown curves represent the training and test phases, and the dark blue curve indicates the delay period in the radial arm-maze task shown in Figure 2A. Left: PCA reduction of the MSUA space. Right: Kernel-PCA reduction of the expanded space containing higher-order activity products. The neural trajectories intermingled on the left become nicely unfolded on the right.

Figure 2. Visualization of task-epoch-specific dynamics.

A. Schema of the delayed win-shift radial arm maze with the definition of separate task epochs (see Materials and Methods for exact definition). B. Three-dimensional projections of the MSUA space combining trials 1 to 5 of animal #1, obtained by PCA (left) and by Multi-Dimensional Scaling (right). C. Three-dimensional projections obtained by a Fisher Discriminant Analysis (FDA) of the training and test choice and reward epochs (multiple classes, centered and normalized for clarity) with the flow field (velocity vectors) indicated by arrows, i.e. these vectors give the magnitude and direction of change of the projected neural activity. Left: MSUA space. Right: Expanded 5 ^th order space (using kernel-FDA). As in B, trials 1–5 of animal #1 were combined for this graph.

Figure 3. Out-of-sample (across trials) predictability of the task-epoch-specific organization of population activity.

A. Statistical analysis of across-trial predictability for animal #1. The predicted SE (SE_predic) is obtained by first constructing a classifier for each pair of task epochs based on a regularized version of Fisher's discriminant criterion exclusively from the first few trials, and then applying it for assigning activity vectors from the last few trials (the test set) to task epochs. SE_predic values averaged across all task-epoch pairs (error bars = SEM) reach a minimum at the rate-interactions order O = 5 and are significantly lower than those obtained for matched bootstrap data (one-sided non-parametric test at p = 0.01). In contrast, the DC-MSUA space (O = 1) does not reveal this predictive structure (p>0.1). Note that chance level is 50% here since a-priori probabilities were set to 0.5 for each pair of task epochs. Reward epochs were excluded from the comparisons due to too few data points. y-axis scale is logarithmic in plots A and C. The asterisk indicates a significant difference in the comparison O = 1 vs. O = 5 for the original data (t-test, Wilcoxon ranksum test, n = 6, both p<0.05; normality assumptions valid according to Lilliefors and Chi-square tests, p>0.12). The regularization penalty was selected such that it provides the minimum SE_predic for different orders O for this particular animal, and then was fixed for all other analyses (see Figure S3 for results obtained with different values of the regularization parameter used in the kernel-FDA). B. Individual comparisons for all task-epoch pairs for the O = 5 space. C. Mean SE_predic averaged across all three recorded animals, attaining a significant minimum at the rate-interactions order O = 5 (Wilcoxon rank-sum test, n = 3 animals, p<0.05). Both forward (from the first to the last set of trials) and backward (from the last to the first set) are shown. Detailed results for animals #2, 3 are shown in Figure 4.

Figure 4. Robustness of across-trials predictability of task-epoch-specific organization of population activity.

Plots show results for different ACC networks (different animals), numbers of recorded units, and sample sizes (numbers of trials). A. Left: Statistical analysis of SE_predic for different numbers of selected units from animal #1. Right: Analysis of SE_predic for animal #1 for different numbers of data points obtained by artificially augmenting or decimating the original data set (by either bootstrapping the original data or randomly removing vectors from it). B. Same for animal #2. C. Same for animal #3. Note that optimal prediction always occurs around similar high-orders of rate interactions as for animal #1 (Figure 3). Asterisks indicate significant differences for the comparisons indicated (Wilcoxon rank-sum test, n = 6, p<0.05 for both animals #2 and #3; nonparametric tests were used because Lilliefors [p<0.003, 0.04] and Chi-square [p<0.003, 0.01] tests indicated that the data significantly deviated from normality, thus violating the assumptions for parametric testing).

Figure 5. Statistical analysis of task-epoch separation in state spaces for the many-animal single-trial data set.

Black solid curves from 8 trials in which animals performed with less than two incorrect arm choices, gray dotted curves from 8 trials where more than four incorrect arm choices were made. A. Task-epoch mean segregation errors (SE) for the good (grey) and bad (black) performance groups averaged across all task-epoch pairs (n = 14, error bars = SEM). Asterisks indicate significant differences for the comparisons indicated. For high-performance animals, a two-tailed non-parametric Wilcoxon rank-sum test was used (n = 14, p<0.04), as data significantly deviated from normality (two-sided Lilliefors test, p<0.03; Chi-square test, p<0.01). For the low-performance group, normality held (Lilliefors test, p>0.44, 0.41), and the comparison between O = 2 and O = 4 conditions is highly significant using either a t-test (p<0.0001) or Wilcoxon ranksum test (p<0.0001). Comparisons between low- and high- performance groups are also significant for O>3 (n = 14; p<0.03, Wilcoxon ranksum test). B. Individual task-epoch-pair comparisons. C. Kullback-Leibler distance between task-epoch distributions averaged across all task-epoch pairs for high- (black) and low- (gray) behavioral performance trials (asterisk and error bars as in A). Task-epoch distributions chart the probabilities of the animal being in a task-epoch C given a population activity vector ν(t), i.e. P(C|Φ(t)). See Materials and Methods for more details.

Figure 6. Convergence of trajectories as assessed from 3-dimensional projections.

As an approximate measure of convergence to task-epoch states the likelihoods of correct classification of population vectors ν(t) into task-epoch sets, i.e. p(ν(t)|Task-Epoch) were charted as a function of the amplitude of the velocity vector in the 3-dimensional PCA projection (determination of velocities directly in the O^th-order spaces is very unreliable due to their high dimensionality; e.g. [44]). In other words, these graphs give the probability density of correct assignment of a neural activity pattern to the right task epoch, or correct-class-likelihood, as a function of the rate of activity change at this point (normalized values across all vectors). Class-likelihoods were based on Bayes-optimal classifiers within the high-dimensional O^th-order spaces and were assessed on test sets of trials (as explained in Figure 3), i.e. refer to out-of sample predictions. Graphs are for increasing rate-interaction orders O from top to bottom. Left: original data; right: bootstrap data (inversion of time). Error bars of insets give 99% confidence intervals. As O increases, lower velocities are associated with higher likelihoods of correct classification, indicating that the neural system dynamic slows down as it approaches the center of such putative attracting sets (see discussion in the main text). Linear fits to the averages of log(P(ν(t)|Task-Epoch)) versus velocity across the 20 bins into which the x-axis was divided (RMS error of fits <1% of the geometric mean; numbers b refer to the slopes of the fits) revealed that differences in slope between the original and bootstrap data were highly significant for O = 5 (p<0.006, t-test, n = 20) but not O = 1 or O = 3. Data shown are for multiple-trial datasets. Insets give the full distributions of data points.

Figure 7. Quantitative assessment of the attracting behavior of task-epoch specific ensemble states within the full high-dimensional spaces.

A. Schema illustrating different types of trajectories which would constitute evidence for an attracting region defined by the task epochs: Trajectory “a” is completely confined within the task-epoch state, trajectory “b” leaves the task-epoch state (for instance, due to perturbation by noise) and then quickly converges back to it, and trajectory “c” is rapidly attracted into the task-epoch state. Black dots in the figure highlight incorrectly classified firing-rate vectors. If only trajectories of types a-c were present, this would strongly suggest that the task-epoch states are indeed attractors. This condition is formally evaluated in C. B. Examples of convergent trajectories, cycling within or returning to the task-epoch states, in the 5^th-order expanded spaces (corresponding to different trials of the task). C. Percentage of trajectories which escape from task-epoch states for the single-trial data sets (red) and as predicted across trials for the multiple-trial data sets (white) within the full high-dimensional O^th-order spaces. A total of ∼20 trajectories was available for each task-epoch specific state during the prediction set of trials. The absence of any trajectories escaping from a bounded region of state space (as defined by the task epochs), i.e. if only trajectories of types a-c were present, would suggest the existence of a basin of attraction which is stable across trials. Asterisk indicates significance for the comparison O = 1 vs. O = 5 (nonparametric Mann-Whitney-U test, p<0.05). Inset: A weaker condition (attracting set condition) will be met if trajectories escaping from the task-epoch set still remain within a trapping region . The graph gives the average percentage of trajectories violating this attracting set definition. Note that task-epoch specific states were defined by narrow (∼1 s) temporal windows around the relevant event such that the majority of available data points are not included in the definition of any one of these states. Hence, the attracting properties revealed here are not just a trivial consequence of a very broad definition of the neural states.