A mathematical model of force transmission from intrafascicularly terminating muscle fibers
- PMID: 21676398
- PMCID: PMC3134549
- DOI: 10.1016/j.jbiomech.2011.04.038
A mathematical model of force transmission from intrafascicularly terminating muscle fibers
Abstract
Many long skeletal muscles are comprised of fibers that terminate intrafascicularly. Force from terminating fibers can be transmitted through shear within the endomysium that surrounds fibers or through tension within the endomysium that extends from fibers to the tendon; however, it is unclear which pathway dominates in force transmission from terminating fibers. The purpose of this work was to develop mathematical models to (i) compare the efficacy of lateral (through shear) and longitudinal (through tension) force transmission in intrafascicularly terminating fibers, and (ii) determine how force transmission is affected by variations in the structure and properties of fibers and the endomysium. The models demonstrated that even though the amount of force that can be transmitted from an intrafascicularly terminating fiber is dependent on fiber resting length (the unstretched length at which passive stress is zero), endomysium shear modulus, and fiber volume fraction (the fraction of the muscle cross-sectional area that is occupied by fibers), fibers that have values of resting length, shear modulus, and volume fraction within physiologic ranges can transmit nearly all of their peak isometric force laterally through shearing of the endomysium. By contrast, the models predicted only limited force transmission ability through tension within the endomysium that extends from the fiber to the tendon. Moreover, when fiber volume fraction decreases to unhealthy ranges (less than 50%), the force-transmitting potential of terminating fibers through shearing of the endomysium decreases significantly. The models presented here support the hypothesis that lateral force transmission through shearing of the endomysium is an effective mode of force transmission in terminating fibers.
Copyright © 2011 Elsevier Ltd. All rights reserved.
Conflict of interest statement
Neither author has any conflict of interest to report in this research.
Figures
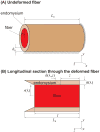






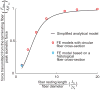
 ), FE models with a circular fiber cross-section (
), FE models with a circular fiber cross-section (
 ) for different fiber resting lengths lengths ranging from 120μm (L0/2r0 = 1.5) to 1.6mm (L0/2r0 = 20), and the FE model of a terminating fiber surrounded by a bundle of fibers created based on a histological cross-section (
) for different fiber resting lengths lengths ranging from 120μm (L0/2r0 = 1.5) to 1.6mm (L0/2r0 = 20), and the FE model of a terminating fiber surrounded by a bundle of fibers created based on a histological cross-section (
 ) with a resting length of 120μm (L0/2r0 = 1.5). In all models the fiber diameter is 80μm, and fiber volume fraction is 75%.
) with a resting length of 120μm (L0/2r0 = 1.5). In all models the fiber diameter is 80μm, and fiber volume fraction is 75%.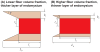
References
-
- Barrett B. The length and mode of termination of individual muscle fibres in the human sartorius and posterior femoral muscles. Acta Anatomica. 1962;48:242–257. - PubMed
-
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. Journal of Biomechanics. 2005;38:657–665. - PubMed
-
- Bloch RJ, Gonzalez-Serratos H. Lateral force transmission across costameres in skeletal muscle. Exercise and Sport Sciences Reviews. 2003;31:73–78. - PubMed
-
- Chan WP, Liu GC. MR imaging of primary skeletal muscle diseases in children. AJR American Journal of Roentgenology. 2002;179:989–997. - PubMed
-
- Claflin DR, Brooks SV. Direct observation of failing fibers in muscles of dystrophic mice provides mechanistic insight into muscular dystrophy. American Journal of Physiology - Cell Physiology. 2008;294:C651–C658. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

