Mixed-model coexpression: calculating gene coexpression while accounting for expression heterogeneity
- PMID: 21685083
- PMCID: PMC3117390
- DOI: 10.1093/bioinformatics/btr221
Mixed-model coexpression: calculating gene coexpression while accounting for expression heterogeneity
Abstract
Motivation: The analysis of gene coexpression is at the core of many types of genetic analysis. The coexpression between two genes can be calculated by using a traditional Pearson's correlation coefficient. However, unobserved confounding effects may cause inflation of the Pearson's correlation so that uncorrelated genes appear correlated. Many general methods have been suggested, which aim to remove the effects of confounding from gene expression data. However, the residual confounding which is not accounted for by these generic correction procedures has the potential to induce correlation between genes. Therefore, a method that specifically aims to calculate gene coexpression between gene expression arrays, while accounting for confounding effects, is desirable.
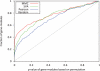
Results: In this article, we present a statistical model for calculating gene coexpression called mixed model coexpression (MMC), which models coexpression within a mixed model framework. Confounding effects are expected to be encoded in the matrix representing the correlation between arrays, the inter-sample correlation matrix. By conditioning on the information in the inter-sample correlation matrix, MMC is able to produce gene coexpressions that are not influenced by global confounding effects and thus significantly reduce the number of spurious coexpressions observed. We applied MMC to both human and yeast datasets and show it is better able to effectively prioritize strong coexpressions when compared to a traditional Pearson's correlation and a Pearson's correlation applied to data corrected with surrogate variable analysis (SVA).
Availability: The method is implemented in the R programming language and may be found at http://genetics.cs.ucla.edu/mmc.
Contact: nfurlott@cs.ucla.edu; eeskin@cs.ucla.edu.
Figures


References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

