Impact of epistasis and pleiotropy on evolutionary adaptation

Abstract

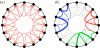
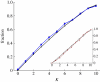
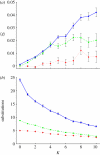
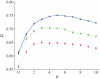
Evolutionary adaptation is often likened to climbing a hill or peak. While this process is simple for fitness landscapes where mutations are independent, the interaction between mutations (epistasis) as well as mutations at loci that affect more than one trait (pleiotropy) are crucial in complex and realistic fitness landscapes. We investigate the impact of epistasis and pleiotropy on adaptive evolution by studying the evolution of a population of asexual haploid organisms (haplotypes) in a model of N interacting loci, where each locus interacts with K other loci. We use a quantitative measure of the magnitude of epistatic interactions between substitutions, and find that it is an increasing function of K. When haplotypes adapt at high mutation rates, more epistatic pairs of substitutions are observed on the line of descent than expected. The highest fitness is attained in landscapes with an intermediate amount of ruggedness that balance the higher fitness potential of interacting genes with their concomitant decreased evolvability. Our findings imply that the synergism between loci that interact epistatically is crucial for evolving genetic modules with high fitness, while too much ruggedness stalls the adaptive process.

Figure 1.

NK model haplotypes for N = 16 and K = 2. For these parameters, the fitness contribution of each locus is determined by interacting with two loci (adjacent in the representation shown here), giving rise to blocks of 2K + 1 interacting genes. (a) Interactions between loci represented by lines, with arrows indicating which loci affect the fitness component of other loci. (b) Actual epistatic interactions on a particular high-fitness peak, where the width of the lines indicates the strength of epistatic interactions (thicker lines equal higher values of ɛ, defined in the main text). Three modules of interacting loci are coloured. The remaining interactions (dashed grey lines) are weak (arrowheads omitted for clarity).

Figure 2.

Schematic illustration of epistasis. Two mutations A and B can interact epistatically in different ways with varying effects on fitness. The fitness of the wild-type is represented by the black baselines, and the heights of arrows represent the fitness after one mutation (W_A or W_B) and after both mutations (W_AB). Green, positive epistasis, red, negative epistasis, black, no epistasis. In (a), two independently beneficial mutations may have their joint effect increased or diminished (W_AB larger or smaller), while in (b) the independent effect of the two mutations is deleterious and beneficial, respectively, and the combined expected effect on fitness is deleterious. In (c), each mutation by itself is deleterious, but when they interact, the result can be reciprocal sign epistasis (green arrow). These sketches illustrate an additive model, where the sum of W_A and W_B is equal to W_AB without epistasis. In our model, using the geometric mean this corresponds to taking the logarithms of the fitness.

Figure 3.

Representative examples of adaptation in single lineages. Fitness on the LOD for a simulation lasting 2000 updates. The adaptive ascent is only shown until the lineage has attained the same fitness as it has after 2000 updates, for N = 20, K = 0 (dashed line) and K = 4 (solid line), at a high mutation rate μ = 10⁻². The inset shows an example LOD at μ = 10⁻⁴, which has only beneficial mutations on the LOD.

Figure 4.

Fraction of epistatic pairs on the LOD. The fraction of mutational pairs on the LOD that interact epistatically (circles) is larger than the numerical pre-selection prediction (crosses) for μ = 10⁻² (p = 0.013672, Wilcoxon signed-rank test). For smaller mutation rates (μ = 10⁻⁴ shown in inset), there is no significant difference from the expectation (p = 0.23242, Wilcoxon signed-rank test). Reversals have been excluded from this analysis. Lines are drawn to guide the eye.

Figure 5.

Fraction of types of the second substitution among all epistatic pairs. Blue, D⁻; green, B⁻; red, D⁺; white, B⁺. Height of bar shows the fraction of all epistatic mutations of a particular type on the LOD for μ = 10⁻². At this mutation rate, a considerable fraction of epistatic substitutions are D⁺ and D⁻, while those fractions are lower for μ = 10⁻³ and 10⁻⁴ (electronic supplementary material, figure S2).

Figure 6.

Mean ɛ and substitutions on the LOD. (a) 〈ɛ〉 on the LOD as defined by equation (2.1). Each datum is the average of 200 LODs and error bars are s.e. Mutation rates are μ = 10⁻² (blue line), μ = 10⁻³ (green dashes) and μ = 10⁻⁴ (red dots). Population size is 5000, N = 20 and the replacement rate is 10%. Lines are drawn to guide the eye. (b) Total number of substitutions as a function of K, mutation rates and colours as in (a).

Figure 7.

Attained fitness Ω as a function of K for three different mutation rates (colours and parameters as in figure 6a) on LOD. K_opt, the point at which Ω is maximal, is larger for higher mutation rates.

Figure 8.

Strength of selection coefficients and epistasis. (a) The effect on fitness of beneficial, s_b (open symbols), and deleterious substitutions, s_d (solid symbols), both increase approximately linearly as a function of K (colours and parameters as in figure 6). (b) Correlation between size of epistasis 〈ɛ〉 and effect of substitutions s, shown here for K = 5 and μ = 10⁻². Reversal substitutions are excluded because they do not contribute to adaptation. Including them would only strengthen the overall correlation. Pearson correlation coefficient r = 0.3549.