Generation of diverse biological forms through combinatorial interactions between tissue polarity and growth
- PMID: 21698124
- PMCID: PMC3116900
- DOI: 10.1371/journal.pcbi.1002071
Generation of diverse biological forms through combinatorial interactions between tissue polarity and growth
Abstract
A major problem in biology is to understand how complex tissue shapes may arise through growth. In many cases this process involves preferential growth along particular orientations raising the question of how these orientations are specified. One view is that orientations are specified through stresses in the tissue (axiality-based system). Another possibility is that orientations can be specified independently of stresses through molecular signalling (polarity-based system). The axiality-based system has recently been explored through computational modelling. Here we develop and apply a polarity-based system which we call the Growing Polarised Tissue (GPT) framework. Tissue is treated as a continuous material within which regionally expressed factors under genetic control may interact and propagate. Polarity is established by signals that propagate through the tissue and is anchored in regions termed tissue polarity organisers that are also under genetic control. Rates of growth parallel or perpendicular to the local polarity may then be specified through a regulatory network. The resulting growth depends on how specified growth patterns interact within the constraints of mechanically connected tissue. This constraint leads to the emergence of features such as curvature that were not directly specified by the regulatory networks. Resultant growth feeds back to influence spatial arrangements and local orientations of tissue, allowing complex shapes to emerge from simple rules. Moreover, asymmetries may emerge through interactions between polarity fields. We illustrate the value of the GPT-framework for understanding morphogenesis by applying it to a growing Snapdragon flower and indicate how the underlying hypotheses may be tested by computational simulation. We propose that combinatorial intractions between orientations and rates of growth, which are a key feature of polarity-based systems, have been exploited during evolution to generate a range of observed biological shapes.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
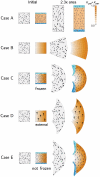
 , orange), POL gradient direction (arrows),
, orange), POL gradient direction (arrows),  organiser (dark blue), and
organiser (dark blue), and  organiser (cyan). Columns 3 and 4 show the state after growth for a certain period. In Cases A, C, the POL gradient, once formed is no longer modified through propagation and deforms with the canvas. In Cases D, the POL gradient is held vertically by an external system. In Case E the POL continues to diffuse so the gradient is continually updated as the shape changes during growth. Deformations of the grid can be compared with the transformations of shape described in . (Mesh of 3200 elements, growth magnitudes around 1 per unit time,
organiser (cyan). Columns 3 and 4 show the state after growth for a certain period. In Cases A, C, the POL gradient, once formed is no longer modified through propagation and deforms with the canvas. In Cases D, the POL gradient is held vertically by an external system. In Case E the POL continues to diffuse so the gradient is continually updated as the shape changes during growth. Deformations of the grid can be compared with the transformations of shape described in . (Mesh of 3200 elements, growth magnitudes around 1 per unit time,  , runtime
, runtime  min for each example.
min for each example.  has arbitrary units.).
has arbitrary units.).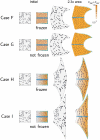
 , runtime
, runtime  5 to 8 min for each example.
5 to 8 min for each example.  has arbitrary units.).
has arbitrary units.).

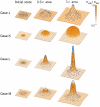
 and
and  . Orange colour denotes the value of specified areal growth. The initially circular discs monitor local shape changes. (B) Shape after growing to 2.2x the area. (C) As (B) but showing regions of resultant anisotropic growth (magenta) and its orientation (lines). (Mesh of 5600 elements, growth magnitudes around 0.018 per unit time,
. Orange colour denotes the value of specified areal growth. The initially circular discs monitor local shape changes. (B) Shape after growing to 2.2x the area. (C) As (B) but showing regions of resultant anisotropic growth (magenta) and its orientation (lines). (Mesh of 5600 elements, growth magnitudes around 0.018 per unit time,  , runtime
, runtime  min for each example.
min for each example.  has arbitrary units. Vertices of the base are fixed in the Z-axis.) (A movie of this development is in ‘Video S1’.).
has arbitrary units. Vertices of the base are fixed in the Z-axis.) (A movie of this development is in ‘Video S1’.).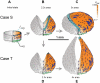
 . (B) Case S. At 2.2x areal growth the sides are arching over. Blue ellipses (induced as circles in initial state) show regions of local anisotropic growth. (C) Arching continues and at 5x areal growth the two sides overlap (there is no collision detection in our current software). (D) Case T. At 2.2x areal growth the distal organiser (cyan) is spatially redistributed to create two small patches causing the orientation of growth to change (arrows) and growth continues upwards (E). (Mesh of 5600 elements, growth magnitudes around 0.018 per unit time,
. (B) Case S. At 2.2x areal growth the sides are arching over. Blue ellipses (induced as circles in initial state) show regions of local anisotropic growth. (C) Arching continues and at 5x areal growth the two sides overlap (there is no collision detection in our current software). (D) Case T. At 2.2x areal growth the distal organiser (cyan) is spatially redistributed to create two small patches causing the orientation of growth to change (arrows) and growth continues upwards (E). (Mesh of 5600 elements, growth magnitudes around 0.018 per unit time,  , runtime
, runtime  min for each example.
min for each example.  has arbitrary units. Vertices of the base are fixed in the Z-axis.) (Movies of these developments, C and D, are in ‘Video S2’ and ‘Video S3’.).
has arbitrary units. Vertices of the base are fixed in the Z-axis.) (Movies of these developments, C and D, are in ‘Video S2’ and ‘Video S3’.).
 and
and  (green and cyan respectively) and cylindrical shape. Orange indicates growth rate parallel to the POL gradient. (B) By the end of the early growth phase, extra ventral growth (dark orange) creates an arch (as in Figure 6). (C) At the beginning of the late phase
(green and cyan respectively) and cylindrical shape. Orange indicates growth rate parallel to the POL gradient. (B) By the end of the early growth phase, extra ventral growth (dark orange) creates an arch (as in Figure 6). (C) At the beginning of the late phase  is formed and anisotropic growth has reoriented along the new axis (arrows show polariser gradient that now points towards
is formed and anisotropic growth has reoriented along the new axis (arrows show polariser gradient that now points towards  , cyan). (D) Adult shape in which the ventral arch has grown upwards (see Section in Fig.1C). (E) Vertical section through adult shape. (F) Similar view of the same model except that anisotropic growth is not reoriented. (Mesh of 3000 elements, growth magnitudes around 0.003 per unit time,
, cyan). (D) Adult shape in which the ventral arch has grown upwards (see Section in Fig.1C). (E) Vertical section through adult shape. (F) Similar view of the same model except that anisotropic growth is not reoriented. (Mesh of 3000 elements, growth magnitudes around 0.003 per unit time,  hours, runtime
hours, runtime  min for each example.
min for each example.  has arbitrary units.) (Movies of these developments, B, C, E, F, are in ‘Video S4’, ‘Video S5’, ‘Video S6’, ‘Video S7’.).
has arbitrary units.) (Movies of these developments, B, C, E, F, are in ‘Video S4’, ‘Video S5’, ‘Video S6’, ‘Video S7’.).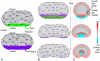
 and
and  on a shape that is polarised from posterior to anterior (arrows). (B) Side view of the developing embryo. The patterns become occluded as the furrow develops. (C) Transverse section of embryo showing colours representing relative specified growth rates perpendicular to the polariser gradient on the internal and external faces. The furrow is produced by a shrinkage on the outside coupled with an expansion on the inside and a net shrinkage in the ventral region (specified by
on a shape that is polarised from posterior to anterior (arrows). (B) Side view of the developing embryo. The patterns become occluded as the furrow develops. (C) Transverse section of embryo showing colours representing relative specified growth rates perpendicular to the polariser gradient on the internal and external faces. The furrow is produced by a shrinkage on the outside coupled with an expansion on the inside and a net shrinkage in the ventral region (specified by  ). Cyan shows negative specified growth on the outside and dark red shows positive growth on the inside. The images are all to the same scale.
). Cyan shows negative specified growth on the outside and dark red shows positive growth on the inside. The images are all to the same scale.
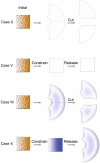

 which is only active on the right side). (C, E) The result of turning off growth, making 8 vertical cuts in the mature shape and allowing the shape to re-stabilise.
which is only active on the right side). (C, E) The result of turning off growth, making 8 vertical cuts in the mature shape and allowing the shape to re-stabilise.
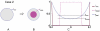
 (blue). (B) The inner region,
(blue). (B) The inner region,  (magenta), is obtained through a combination of diffusion and interaction of a signal (
(magenta), is obtained through a combination of diffusion and interaction of a signal ( ) produced by
) produced by  . (C) Profiles of the factors (
. (C) Profiles of the factors ( ,
,  ,
,  ) plotted along a diameter together with the thresholds,
) plotted along a diameter together with the thresholds,  and
and  .
.References
-
- Wolpert L, Tickle C. U S A: Oxford University Press; 2010. Principles of Development.720 4th edition.
-
- Gilbert SF. Sinauer Associates Inc.; 2010. Developmental Biology.711 9th edition.
-
- Murray JD. A pre-pattern formation mechanism for animal coat markings. J Theor Biol. 1981;88:161–199.
-
- Murray JD, Maini PK, Tranquillo RT. Mechanochemical models for generating biological pattern and form in development. Phys Rep. 1988;171:59–84.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

