Mixed Membership Stochastic Blockmodels
- PMID: 21701698
- PMCID: PMC3119541
Mixed Membership Stochastic Blockmodels
Abstract
Observations consisting of measurements on relationships for pairs of objects arise in many settings, such as protein interaction and gene regulatory networks, collections of author-recipient email, and social networks. Analyzing such data with probabilisic models can be delicate because the simple exchangeability assumptions underlying many boilerplate models no longer hold. In this paper, we describe a latent variable model of such data called the mixed membership stochastic blockmodel. This model extends blockmodels for relational data to ones which capture mixed membership latent relational structure, thus providing an object-specific low-dimensional representation. We develop a general variational inference algorithm for fast approximate posterior inference. We explore applications to social and protein interaction networks.
Figures


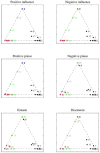


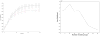



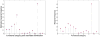


References
-
- Airoldi EM, Blei DM, Xing EP, Fienberg SE. ACM SIGKDD Workshop on Link Discovery: Issues, Approaches and Applications. 2005. A latent mixed-membership model for relational data.
-
- Airoldi EM, Fienberg SE, Joutard C, Love TM. Technical Report CMU-ML-06-101. School of Computer Science, Carnegie Mellon University; Apr, 2006a. Discovering latent patterns with hierarchical Bayesian mixed-membership models and the issue of model choice.
-
- Airoldi EM, Fienberg SE, Xing EP. Biological context analysis of gene expression data. Jun, 2006b. Manuscript.
-
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. 4th. Garland: 2002.
-
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubinand GM, Sherlock G. Gene ontology: Tool for the unification of biology. The gene ontology consortium. Nature Genetics. 2000;25(1):25–29. - PMC - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
