Moire bands in twisted double-layer graphene
- PMID: 21730173
- PMCID: PMC3145708
- DOI: 10.1073/pnas.1108174108
Moire bands in twisted double-layer graphene
Abstract
A moiré pattern is formed when two copies of a periodic pattern are overlaid with a relative twist. We address the electronic structure of a twisted two-layer graphene system, showing that in its continuum Dirac model the moiré pattern periodicity leads to moiré Bloch bands. The two layers become more strongly coupled and the Dirac velocity crosses zero several times as the twist angle is reduced. For a discrete set of magic angles the velocity vanishes, the lowest moiré band flattens, and the Dirac-point density-of-states and the counterflow conductivity are strongly enhanced.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 and
and  . The circles represent Dirac points of the rotated graphene layers, separated by kθ = 2kD sin(θ/2), where kD is the magnitude of the Brillouin-zone corner wave vector for a single layer. Conservation of crystal momentum implies that p′ = k + qb for a tunneling process in the vicinity of the plotted Dirac points. (B) The three equivalent Dirac points in the first Brillouin zone result in three distinct hopping processes. Interference between hopping processes with different wave vectors captures the spatial variation of interlayer coordination that defines the moiré pattern. For all the three processes |qj| = kθ; however, the hopping directions are (0,-1) for j = 1,
. The circles represent Dirac points of the rotated graphene layers, separated by kθ = 2kD sin(θ/2), where kD is the magnitude of the Brillouin-zone corner wave vector for a single layer. Conservation of crystal momentum implies that p′ = k + qb for a tunneling process in the vicinity of the plotted Dirac points. (B) The three equivalent Dirac points in the first Brillouin zone result in three distinct hopping processes. Interference between hopping processes with different wave vectors captures the spatial variation of interlayer coordination that defines the moiré pattern. For all the three processes |qj| = kθ; however, the hopping directions are (0,-1) for j = 1,  for j = 2, and
for j = 2, and  for j = 3. We interchangeably use 1, 2, 3, b, tr, and tl as subscripts for the three momentum transfers qj. Repeated hopping generates a k-space honeycomb lattice. The green solid line marks the moiré band Wigner–Seitz cell. In a repeated zone scheme the red and black circles mark the Dirac points of the two layers.
for j = 3. We interchangeably use 1, 2, 3, b, tr, and tl as subscripts for the three momentum transfers qj. Repeated hopping generates a k-space honeycomb lattice. The green solid line marks the moiré band Wigner–Seitz cell. In a repeated zone scheme the red and black circles mark the Dirac points of the two layers.

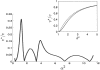

 , where kθ = 2kD sin(θ/2) with kD being the Dirac wave vector. Blue dots denote areas with local AB coordination. (Left) Smallest positive energy of the interlayer Hamiltonian. The energy vanishes for local AB or BA coordination and reached a maximum of 3w for local AA coordination.
, where kθ = 2kD sin(θ/2) with kD being the Dirac wave vector. Blue dots denote areas with local AB coordination. (Left) Smallest positive energy of the interlayer Hamiltonian. The energy vanishes for local AB or BA coordination and reached a maximum of 3w for local AA coordination.References
-
- McCann E, Falko VI. Landau-level degeneracy and quantum hall effect in a graphite bilayer. Phys Rev Lett. 2006;96:086805. - PubMed
-
- Koshino M, Ando T. Orbital diamagnetism in multilayer graphenes: Systematic study with the effective mass approximation. Phys Rev B. 2007;76:085425.
-
- Nilsson J, Castro Neto AH, Guinea F, Peres NMR. Electronic properties of bilayer and multilayer graphene. Phys Rev B. 2008;78:045405.
-
- Min H, MacDonald AH. Chiral decomposition in the electronic structure of graphene multilayers. Phys Rev B. 2008;77:155416.
-
- Koshino M, McCann E. Trigonal warping and Berrys phase Nπ in ABC-stacked multilayer graphene. Phys Rev B. 2009;80:165409.
LinkOut - more resources
Full Text Sources
Other Literature Sources

