Generative embedding for model-based classification of fMRI data

Abstract

Decoding models, such as those underlying multivariate classification algorithms, have been increasingly used to infer cognitive or clinical brain states from measures of brain activity obtained by functional magnetic resonance imaging (fMRI). The practicality of current classifiers, however, is restricted by two major challenges. First, due to the high data dimensionality and low sample size, algorithms struggle to separate informative from uninformative features, resulting in poor generalization performance. Second, popular discriminative methods such as support vector machines (SVMs) rarely afford mechanistic interpretability. In this paper, we address these issues by proposing a novel generative-embedding approach that incorporates neurobiologically interpretable generative models into discriminative classifiers. Our approach extends previous work on trial-by-trial classification for electrophysiological recordings to subject-by-subject classification for fMRI and offers two key advantages over conventional methods: it may provide more accurate predictions by exploiting discriminative information encoded in 'hidden' physiological quantities such as synaptic connection strengths; and it affords mechanistic interpretability of clinical classifications. Here, we introduce generative embedding for fMRI using a combination of dynamic causal models (DCMs) and SVMs. We propose a general procedure of DCM-based generative embedding for subject-wise classification, provide a concrete implementation, and suggest good-practice guidelines for unbiased application of generative embedding in the context of fMRI. We illustrate the utility of our approach by a clinical example in which we classify moderately aphasic patients and healthy controls using a DCM of thalamo-temporal regions during speech processing. Generative embedding achieves a near-perfect balanced classification accuracy of 98% and significantly outperforms conventional activation-based and correlation-based methods. This example demonstrates how disease states can be detected with very high accuracy and, at the same time, be interpreted mechanistically in terms of abnormalities in connectivity. We envisage that future applications of generative embedding may provide crucial advances in dissecting spectrum disorders into physiologically more well-defined subgroups.

Figure 1. Conceptual overview of generative embedding for fMRI.

This schematic illustrates the key principles by which generative embedding enables model-based classification for functional magnetic resonance imaging (fMRI). Initially, each subject is represented by a measure of blood oxygen level dependent (BOLD) activity with one temporal and three spatial dimensions. In the first analysis step (model inversion), these subject-specific data are used to estimate the parameters of a generative model, which represents a mapping of the data onto a probability distribution in a parametric family (see Sections ‘DCM for fMRI’ and ‘Model inversion’). In the second step (kernel construction), a kernel function is defined that represents a similarity metric between any two fitted models and . This step can be split up into an initial mapping followed by a conventional kernel . The kernel implies a generative score space (or model-based feature space; see Section ‘Kernel construction’), which provides a comprehensive statistical representation of every subject. In this illustrative participant, the influence of region A on region B as well as the self-connection of region B were particularly strong. In the third step, a classifier is used to find a separating hyperplane between groups of subjects, based exclusively on their model-based representations (see Section ‘Classification’). When using a linear kernel, each feature corresponds to the coupling strength between two regions, which, in the fourth step, enables a mechanistic interpretation of feature weights in the context of the underlying model (see Section ‘Interpretation of the feature space’). Here, the influence of A on B and C were jointly most informative in distinguishing between groups. For a concrete implementation of this procedure, see Figure 2.

Figure 2. Strategies for unbiased DCM-based generative embedding.

This figure illustrates how generative embedding can be implemented using dynamic causal modelling. Depending on whether regions of interest are defined anatomically, based on across-subjects functional contrasts, or based on between-group contrasts, there are several possible practical procedures. Some of these procedures may lead to biased estimates of classification accuracy (grey boxes). Procedures a, c, and f avoid this bias, and are therefore recommended (green boxes). The analysis of the illustrative dataset described in this paper follows procedure c.

Figure 3. Dynamic causal model of speech processing.

The diagram illustrates the specific dynamic causal model (DCM) that was used for the illustrative application of generative embedding in this study. It consists of 6 regions (circles), 15 interregional connections (straight arrows between regions), 6 self-connections (circular arrows), and 2 stimulus inputs (straight arrows at the bottom). The specific set of connections shown here is the result of Bayesian model selection that was carried out on the basis of a large set of competing connectivity layouts (for details, see Schofield et al., in preparation). A sparse set of 9 out of 23 connectivity and input parameters (see Figure 10) was found to be sufficiently informative to distinguish between aphasic patients and healthy controls with near-perfect accuracy (see Figure 5). The connections corresponding to these 9 parameters are highlighted in red. Only three parameters were selected in all cross-validation folds and are thus particularly meaningful for classification (bold red arrows); these refer to connections mediating information transfer from the right to the left hemisphere, converging on left PT, which is a key structure in speech processing.

Figure 4. Practical implementation of generative embedding for fMRI.

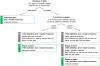
This figure summarizes the three core steps involved in the practical implementation of generative embedding proposed in this paper. This procedure integrates the inversion of a generative model into cross-validation. In step 1, within a given repetition , the model is specified using all subjects except . This yields a set of time series for each subject . In step 2, the model is inverted independently for each subject, giving rise to a set of subject-specific posterior parameter means . In step 3, these parameter estimates are used to train a classifier on all subjects except and test it on subject , which yields a prediction about the class label of subject . 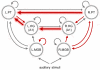After having repeated these three steps for all , the set of predicted labels can be compared with the true labels, which allows us to estimate the algorithm's generalization performance. In addition, parameters that proved jointly discriminative can be interpreted in the context of the underlying generative model. The sequence of steps shown here corresponds to the procedure shown in Figure 2c and 2f, where it is contrasted with alternative procedures that are simpler but risk an optimistic bias in estimating generalization performance.

Figure 5. Biologically unlikely alternative models.

To illustrate the specificity of generative embedding, the analysis described in the main text was repeated on the basis of three biologically less plausible models. In contrast to the full model shown in Figure 3, these alternative models either (a) contained no feedback or interhemispheric connections, (b) accounted for activity in the left hemisphere only, or (c) focussed exclusively on the right hemisphere. For results, see Table 2 and Figure 6.

Figure 6. Classification performance.

Classification based on generative embedding using the model shown in Figure 3 was compared to ten alternative methods: anatomical feature selection, contrast feature selection, searchlight feature selection, PCA-based dimensionality reduction, regional correlations based on region means, regional correlations based on eigenvariates, regional z-transformed correlations based on eigenvariates, as well as generative embedding using three biologically unlikely alternative models (see inset legends for abbreviations). (a) The balanced accuracy and its central 95% posterior probability interval show that all methods performed significantly better than chance (50%) with the exception of classification with anatomical feature selection and generative embedding using a nonsensical model. Differences between activation-based methods (light grey) and correlation-based methods (dark grey) were largely statistically indistinguishable. By contrast, using the full model shown in Figure 3, generative embedding (blue) significantly outperformed all other methods, except when used with biologically unlikely models (Figure 5). (b) Receiver-operating characteristic (ROC) curves of the eleven methods illustrate the trade-off between true positive rate (sensitivity) and false positive rate (1 – specificity) across the entire range of detection thresholds. A larger area under the curve is better. (c) Precision-recall (PR) curves illustrate the trade-off between positive prediction value (precision) and true positive rate (recall). A larger area under the curve is better. Smooth ROC and PR curves were obtained using a binormal assumption on the underlying decision values . For a numerical summary of all results, see Table 2.

Figure 7. Induction of a generative score space.

This figure provides an intuition of how a generative model transforms the data from a voxel-based feature space into a generative score space (or model-based feature space), in which classes become more separable. The left plot shows how aphasic patients (red) and healthy controls (grey) are represented in voxel space, based on t-scores from a simple ‘all auditory events’ contrast (see main text). The three axes represent the peaks of those three clusters that showed the strongest discriminability between patients and controls, based on a locally multivariate searchlight classification analysis. They are located in L.PT, L.HG, and R.PT, respectively (cf. Table 1). The right plot shows the three individually most discriminative parameters (two-sample t-test) in the (normalized) generative score space induced by a dynamic causal model of speech processing (see Figure 3). The plot illustrates how aphasic patients and healthy controls become almost perfectly linearly separable in the new space. Note that this figure is based on normalized examples (as used by the classifier), which means the marginal densities are not the same as those shown in Figure 9 but are exactly those seen by the classifier. A stereogram of the generative score space can be found in the Supplementary Material (Figure S4).

Figure 8. Connectional fingerprints.

Given the low dimensionality of the model-induced feature space, subjects can be visualized in terms of ‘connectional fingerprints’ that are based on a simple radial coordinate system in which each axis corresponds to the maximum a posteriori (MAP) estimate of a particular model parameter. The plot shows that the difference between aphasic patients (red) and healthy controls (grey) is not immediately obvious, suggesting that it might be subtle and potentially of a distributed nature.

Figure 9. Univariate feature densities.

Separately for patients (red) and healthy controls (grey), the figure shows nonparametric estimates of the class-conditional densities of the maximum a posteriori (MAP) estimates of model parameters. The estimates themselves are shown as a rug along the x-axis. The results of individual (uncorrected) two-sample t-tests, thresholded at p = 0.05, are indicated in the title of each diagram. Three stars (***) correspond to p<0.001, indicating that the associated model parameter assumes very different values for patients and controls.

Figure 10. Discriminative features.

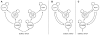
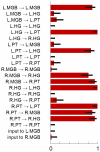
A support vector machine with a sparsity-inducing regularizer (capped -regularizer) was trained and tested in a leave-one-out cross-validation scheme, resulting in subsets of selected features. The figure summarizes these subsets by visualizing how often each feature (printed along the y-axis) was selected across the repetitions (given as a fraction on the x-axis). Error bars represent central 95% posterior probability intervals of a Beta distribution with a flat prior over the interval [0, 1]. A group of 9 features was consistently found jointly informative for discriminating between aphasic patients and healthy controls (see main text). An additional figure showing which features were selected in each cross-validation fold can be found in the Supplementary Material (Figure S3). Crucially, since each feature corresponds to a model parameter that describes one particular interregional connection strength, the group of informative features can be directly related back to the underlying dynamic causal model (see highlighted connections in Figure 3).