Unravelling transmission trees of infectious diseases by combining genetic and epidemiological data
- PMID: 21733899
- PMCID: PMC3234549
- DOI: 10.1098/rspb.2011.0913
Unravelling transmission trees of infectious diseases by combining genetic and epidemiological data
Abstract
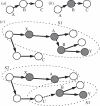
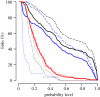
Knowledge on the transmission tree of an epidemic can provide valuable insights into disease dynamics. The transmission tree can be reconstructed by analysing either detailed epidemiological data (e.g. contact tracing) or, if sufficient genetic diversity accumulates over the course of the epidemic, genetic data of the pathogen. We present a likelihood-based framework to integrate these two data types, estimating probabilities of infection by taking weighted averages over the set of possible transmission trees. We test the approach by applying it to temporal, geographical and genetic data on the 241 poultry farms infected in an epidemic of avian influenza A (H7N7) in The Netherlands in 2003. We show that the combined approach estimates the transmission tree with higher correctness and resolution than analyses based on genetic or epidemiological data alone. Furthermore, the estimated tree reveals the relative infectiousness of farms of different types and sizes.
Figures


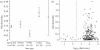
References
-
- Keeling M. J., Woolhouse M. E., May R. M., Davies G., Grenfell B. T. 2003. Modelling vaccination strategies against foot-and-mouth disease. Nature 421, 136–14210.1038/nature01343 (doi:10.1038/nature01343) - DOI - DOI - PubMed
-
- Ferguson N. M., Donnelly C. A., Anderson R. M. 2001. Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain. Nature 413, 542–54810.1038/35097116 (doi:10.1038/35097116) - DOI - DOI - PubMed
-
- Heijne J. C., Teunis P., Morroy G., Wijkmans C., Oostveen S., Duizer E., Kretzschmar M., Wallinga J. 2009. Enhanced hygiene measures and norovirus transmission during an outbreak. Emerg. Infect. Dis. 15, 24–3010.3201/1501.080299 (doi:10.3201/1501.080299) - DOI - DOI - PMC - PubMed
-
- Wallinga J., Teunis P. 2004. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 160, 509–51610.1093/aje/kwh255 (doi:10.1093/aje/kwh255) - DOI - DOI - PMC - PubMed
-
- Lloyd-Smith J. O., Schreiber S. J., Kopp P. E., Getz W. M. 2005. Superspreading and the effect of individual variation on disease emergence. Nature 438, 355–35910.1038/nature04153 (doi:10.1038/nature04153) - DOI - DOI - PMC - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

