Two-dimensional adaptation in the auditory forebrain
- PMID: 21753019
- PMCID: PMC3296429
- DOI: 10.1152/jn.00905.2010
Two-dimensional adaptation in the auditory forebrain
Abstract
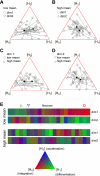
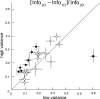
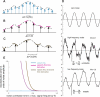
Sensory neurons exhibit two universal properties: sensitivity to multiple stimulus dimensions, and adaptation to stimulus statistics. How adaptation affects encoding along primary dimensions is well characterized for most sensory pathways, but if and how it affects secondary dimensions is less clear. We studied these effects for neurons in the avian equivalent of primary auditory cortex, responding to temporally modulated sounds. We showed that the firing rate of single neurons in field L was affected by at least two components of the time-varying sound log-amplitude. When overall sound amplitude was low, neural responses were based on nonlinear combinations of the mean log-amplitude and its rate of change (first time differential). At high mean sound amplitude, the two relevant stimulus features became the first and second time derivatives of the sound log-amplitude. Thus a strikingly systematic relationship between dimensions was conserved across changes in stimulus intensity, whereby one of the relevant dimensions approximated the time differential of the other dimension. In contrast to stimulus mean, increases in stimulus variance did not change relevant dimensions, but selectively increased the contribution of the second dimension to neural firing, illustrating a new adaptive behavior enabled by multidimensional encoding. Finally, we demonstrated theoretically that inclusion of time differentials as additional stimulus features, as seen so prominently in the single-neuron responses studied here, is a useful strategy for encoding naturalistic stimuli, because it can lower the necessary sampling rate while maintaining the robustness of stimulus reconstruction to correlated noise.
Figures


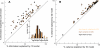





Similar articles
-
Aging Affects Adaptation to Sound-Level Statistics in Human Auditory Cortex.J Neurosci. 2018 Feb 21;38(8):1989-1999. doi: 10.1523/JNEUROSCI.1489-17.2018. Epub 2018 Jan 22. J Neurosci. 2018. PMID: 29358362 Free PMC article.
-
Spectral tuning of adaptation supports coding of sensory context in auditory cortex.PLoS Comput Biol. 2019 Oct 18;15(10):e1007430. doi: 10.1371/journal.pcbi.1007430. eCollection 2019 Oct. PLoS Comput Biol. 2019. PMID: 31626624 Free PMC article.
-
Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds.Exp Brain Res. 1996 Mar;108(2):273-84. doi: 10.1007/BF00228100. Exp Brain Res. 1996. PMID: 8815035
-
An overview of stimulus-specific adaptation in the auditory thalamus.Brain Topogr. 2014 Jul;27(4):480-99. doi: 10.1007/s10548-013-0342-6. Epub 2013 Dec 17. Brain Topogr. 2014. PMID: 24343247 Review.
-
Sensitivity and selectivity of neurons in auditory cortex to the pitch, timbre, and location of sounds.Neuroscientist. 2010 Aug;16(4):453-69. doi: 10.1177/1073858410371009. Epub 2010 Jun 7. Neuroscientist. 2010. PMID: 20530254 Review.
Cited by
-
A neural mechanism for time-window separation resolves ambiguity of adaptive coding.PLoS Biol. 2015 Mar 11;13(3):e1002096. doi: 10.1371/journal.pbio.1002096. eCollection 2015 Mar. PLoS Biol. 2015. PMID: 25761097 Free PMC article.
-
Nonlinear computations underlying temporal and population sparseness in the auditory system of the grasshopper.J Neurosci. 2012 Jul 18;32(29):10053-62. doi: 10.1523/JNEUROSCI.5911-11.2012. J Neurosci. 2012. PMID: 22815519 Free PMC article.
-
Identifying functional bases for multidimensional neural computations.Neural Comput. 2013 Jul;25(7):1870-90. doi: 10.1162/NECO_a_00465. Epub 2013 Apr 22. Neural Comput. 2013. PMID: 23607565 Free PMC article.
-
Constructing noise-invariant representations of sound in the auditory pathway.PLoS Biol. 2013 Nov;11(11):e1001710. doi: 10.1371/journal.pbio.1001710. Epub 2013 Nov 12. PLoS Biol. 2013. PMID: 24265596 Free PMC article.
-
Large-scale synchronized activity during vocal deviance detection in the zebra finch auditory forebrain.J Neurosci. 2012 Aug 1;32(31):10594-608. doi: 10.1523/JNEUROSCI.6045-11.2012. J Neurosci. 2012. PMID: 22855809 Free PMC article.
References
-
- Abramowitz M, Stegun IA. Handbook of Mathematical Functions. Washington, DC: US Government Printing Office, 1964
-
- Adelman TL, Bialek W, Olberg RM. The information content of receptive fields. Neuron 40: 823–833, 2003 - PubMed
-
- Agüera y Arcas B, Fairhall AL. What causes a neuron to spike? Neural Comput 15: 1789–1807, 2003 - PubMed
-
- Agüera y Arcas B, Fairhall AL, Bialek W. Computation in a single neuron: Hodgkin and Huxley revisited. Neural Comput 15: 1715–1749, 2003 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

