Resolution of the stochastic strategy spatial prisoner's dilemma by means of particle swarm optimization
- PMID: 21760906
- PMCID: PMC3131296
- DOI: 10.1371/journal.pone.0021787
Resolution of the stochastic strategy spatial prisoner's dilemma by means of particle swarm optimization
Abstract
We study the evolution of cooperation among selfish individuals in the stochastic strategy spatial prisoner's dilemma game. We equip players with the particle swarm optimization technique, and find that it may lead to highly cooperative states even if the temptations to defect are strong. The concept of particle swarm optimization was originally introduced within a simple model of social dynamics that can describe the formation of a swarm, i.e., analogous to a swarm of bees searching for a food source. Essentially, particle swarm optimization foresees changes in the velocity profile of each player, such that the best locations are targeted and eventually occupied. In our case, each player keeps track of the highest payoff attained within a local topological neighborhood and its individual highest payoff. Thus, players make use of their own memory that keeps score of the most profitable strategy in previous actions, as well as use of the knowledge gained by the swarm as a whole, to find the best available strategy for themselves and the society. Following extensive simulations of this setup, we find a significant increase in the level of cooperation for a wide range of parameters, and also a full resolution of the prisoner's dilemma. We also demonstrate extreme efficiency of the optimization algorithm when dealing with environments that strongly favor the proliferation of defection, which in turn suggests that swarming could be an important phenomenon by means of which cooperation can be sustained even under highly unfavorable conditions. We thus present an alternative way of understanding the evolution of cooperative behavior and its ubiquitous presence in nature, and we hope that this study will be inspirational for future efforts aimed in this direction.
Conflict of interest statement
Figures
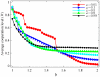
 ) might be beneficial at low temptations to defect, imitating personal success (
) might be beneficial at low temptations to defect, imitating personal success ( ) is definitively better for the evolution of cooperation in strongly defection-prone environments. Each data point is an average of the final outcome (stationary state) of the game over
) is definitively better for the evolution of cooperation in strongly defection-prone environments. Each data point is an average of the final outcome (stationary state) of the game over  independent realizations. Lines connecting the symbols are just to guide the eye.
independent realizations. Lines connecting the symbols are just to guide the eye.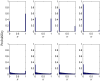
 the nature of the stochastic strategy prisoner's dilemma game is essentially completely overridden by the selfish drive of players to reach the highest current payoffs in the swarm, in turn virtually completely transforming the game to its two-strategy [only
the nature of the stochastic strategy prisoner's dilemma game is essentially completely overridden by the selfish drive of players to reach the highest current payoffs in the swarm, in turn virtually completely transforming the game to its two-strategy [only  (full defection) or
(full defection) or  (full cooperation) strategies are present in the population] version. Conversely, for
(full cooperation) strategies are present in the population] version. Conversely, for  the full spectrum of available strategies is exploited to arrive at the final stationary state. Note that the horizontal axis displays the willingness to cooperate
the full spectrum of available strategies is exploited to arrive at the final stationary state. Note that the horizontal axis displays the willingness to cooperate  (defining the strategy of every player), while the vertical axis depicts the probability that this strategy is present in the population. Depicted results are averages of the final outcome (stationary state) over
(defining the strategy of every player), while the vertical axis depicts the probability that this strategy is present in the population. Depicted results are averages of the final outcome (stationary state) over  independent realizations.
independent realizations.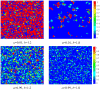
 only the two “extreme” strategies (with rare exceptions) are adopted, while for high values of
only the two “extreme” strategies (with rare exceptions) are adopted, while for high values of  the whole array of available strategies comes into play. Moreover, it is interesting to observe that values of
the whole array of available strategies comes into play. Moreover, it is interesting to observe that values of  yield the well-known clustering of cooperators on the square lattice, while the snapshots for
yield the well-known clustering of cooperators on the square lattice, while the snapshots for  seem to have these feature somewhat less pronounced, although still clearly inferable (note that the distinction of clusters is somewhat difficult due to the continuous array of possible strategies). This suggests that, besides the clustering of cooperators, additional mechanisms may underlie the survival of cooperators at high temptations to defect and
seem to have these feature somewhat less pronounced, although still clearly inferable (note that the distinction of clusters is somewhat difficult due to the continuous array of possible strategies). This suggests that, besides the clustering of cooperators, additional mechanisms may underlie the survival of cooperators at high temptations to defect and  within the present setup. The color encoding, as depicted right, indicates the values of
within the present setup. The color encoding, as depicted right, indicates the values of  for each individual player.
for each individual player.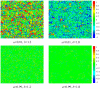
 , while bottom row features results for
, while bottom row features results for  . Irrespective of
. Irrespective of  , it can be observed that for
, it can be observed that for  the whole population essentially becomes a swarm in that the velocities of all players are much the same and close to zero. The fact that the prevailing velocity is close to zero simply reflects that the stationary state has been reached by means of adaptive, locally-inspired and slow strategy changes (which are, however, very effective even if the temptations to defect are strong). For
the whole population essentially becomes a swarm in that the velocities of all players are much the same and close to zero. The fact that the prevailing velocity is close to zero simply reflects that the stationary state has been reached by means of adaptive, locally-inspired and slow strategy changes (which are, however, very effective even if the temptations to defect are strong). For  , however, only isolated clusters can be considered to act as swarms, while the majority of players cannot be associated with any kind of group dynamics and is simply caught in the futile pursuit for the highest, yet for the majority unattainable, payoffs. These results indicate that swarming is an important agonist that promotes cooperation at high temptations to defect (see results presented in Fig. 1). The color encoding, as depicted right, indicates the values of
, however, only isolated clusters can be considered to act as swarms, while the majority of players cannot be associated with any kind of group dynamics and is simply caught in the futile pursuit for the highest, yet for the majority unattainable, payoffs. These results indicate that swarming is an important agonist that promotes cooperation at high temptations to defect (see results presented in Fig. 1). The color encoding, as depicted right, indicates the values of  for each individual player, where
for each individual player, where  was chosen sufficiently large such that the stationary state of the game has been reached. Importantly, we note that for
was chosen sufficiently large such that the stationary state of the game has been reached. Importantly, we note that for  the stationary state has in fact been reached, although at a given instance in time the average velocity in the population might be different from zero.
the stationary state has in fact been reached, although at a given instance in time the average velocity in the population might be different from zero.Similar articles
-
Transforming the dilemma.Evolution. 2007 Oct;61(10):2281-92. doi: 10.1111/j.1558-5646.2007.00196.x. Epub 2007 Aug 17. Evolution. 2007. PMID: 17711471 Free PMC article.
-
Stochastic dynamics of the prisoner's dilemma with cooperation facilitators.Phys Rev E Stat Nonlin Soft Matter Phys. 2012 Jul;86(1 Pt 1):011134. doi: 10.1103/PhysRevE.86.011134. Epub 2012 Jul 30. Phys Rev E Stat Nonlin Soft Matter Phys. 2012. PMID: 23005395
-
Comment on "Stochastic dynamics of the prisoner's dilemma with cooperation facilitators".Phys Rev E Stat Nonlin Soft Matter Phys. 2013 Oct;88(4):046101. doi: 10.1103/PhysRevE.88.046101. Epub 2013 Oct 31. Phys Rev E Stat Nonlin Soft Matter Phys. 2013. PMID: 24229312
-
Spatialization and greater generosity in the stochastic Prisoner's Dilemma.Biosystems. 1996;37(1-2):3-17. doi: 10.1016/0303-2647(95)01541-8. Biosystems. 1996. PMID: 8924636 Review.
-
Resolving the iterated prisoner's dilemma: theory and reality.J Evol Biol. 2011 Aug;24(8):1628-39. doi: 10.1111/j.1420-9101.2011.02307.x. Epub 2011 May 23. J Evol Biol. 2011. PMID: 21599777 Review.
Cited by
-
A Hybrid Multi-Objective Particle Swarm Optimization with Central Control Strategy.Comput Intell Neurosci. 2022 Mar 9;2022:1522096. doi: 10.1155/2022/1522096. eCollection 2022. Comput Intell Neurosci. 2022. PMID: 35310587 Free PMC article.
-
Swarm intelligence inspired shills and the evolution of cooperation.Sci Rep. 2014 Jun 9;4:5210. doi: 10.1038/srep05210. Sci Rep. 2014. PMID: 24909519 Free PMC article.
-
A hybrid search algorithm for swarm robots searching in an unknown environment.PLoS One. 2014 Nov 11;9(11):e111970. doi: 10.1371/journal.pone.0111970. eCollection 2014. PLoS One. 2014. PMID: 25386855 Free PMC article.
-
Transformer Incipient Fault Prediction Using Combined Artificial Neural Network and Various Particle Swarm Optimisation Techniques.PLoS One. 2015 Jun 23;10(6):e0129363. doi: 10.1371/journal.pone.0129363. eCollection 2015. PLoS One. 2015. PMID: 26103634 Free PMC article.
References
-
- Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge: Cambridge Univ Press; 1998.
-
- Nowak MA. Evolutionary Dynamics. Cambridge, MA: Harvard University Press; 2006.
-
- Sigmund K. The Calculus of Selfishness. Princeton, MA: Princeton University Press; 2010.
-
- Hardin G. The tragedy of the commons. Science. 1968;162:1243–1248. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

