Resolution of the stochastic strategy spatial prisoner's dilemma by means of particle swarm optimization

Abstract

We study the evolution of cooperation among selfish individuals in the stochastic strategy spatial prisoner's dilemma game. We equip players with the particle swarm optimization technique, and find that it may lead to highly cooperative states even if the temptations to defect are strong. The concept of particle swarm optimization was originally introduced within a simple model of social dynamics that can describe the formation of a swarm, i.e., analogous to a swarm of bees searching for a food source. Essentially, particle swarm optimization foresees changes in the velocity profile of each player, such that the best locations are targeted and eventually occupied. In our case, each player keeps track of the highest payoff attained within a local topological neighborhood and its individual highest payoff. Thus, players make use of their own memory that keeps score of the most profitable strategy in previous actions, as well as use of the knowledge gained by the swarm as a whole, to find the best available strategy for themselves and the society. Following extensive simulations of this setup, we find a significant increase in the level of cooperation for a wide range of parameters, and also a full resolution of the prisoner's dilemma. We also demonstrate extreme efficiency of the optimization algorithm when dealing with environments that strongly favor the proliferation of defection, which in turn suggests that swarming could be an important phenomenon by means of which cooperation can be sustained even under highly unfavorable conditions. We thus present an alternative way of understanding the evolution of cooperative behavior and its ubiquitous presence in nature, and we hope that this study will be inspirational for future efforts aimed in this direction.

Figure 1. Average level of cooperation in dependence on for different values of .

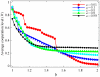
It can be observed that while imitating the best performing player in the swarm () might be beneficial at low temptations to defect, imitating personal success () is definitively better for the evolution of cooperation in strongly defection-prone environments. Each data point is an average of the final outcome (stationary state) of the game over independent realizations. Lines connecting the symbols are just to guide the eye.

Figure 2. Distribution of strategies in the whole population, as obtained for different combinations of and .

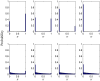
It can be observed that for the nature of the stochastic strategy prisoner's dilemma game is essentially completely overridden by the selfish drive of players to reach the highest current payoffs in the swarm, in turn virtually completely transforming the game to its two-strategy [only (full defection) or (full cooperation) strategies are present in the population] version. Conversely, for the full spectrum of available strategies is exploited to arrive at the final stationary state. Note that the horizontal axis displays the willingness to cooperate (defining the strategy of every player), while the vertical axis depicts the probability that this strategy is present in the population. Depicted results are averages of the final outcome (stationary state) over independent realizations.

Figure 3. Characteristic spatial distributions of strategies, as obtained for different combinations of and .

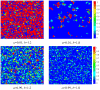
As concluded from results depicted in Fig. 2, for low values of only the two “extreme” strategies (with rare exceptions) are adopted, while for high values of the whole array of available strategies comes into play. Moreover, it is interesting to observe that values of yield the well-known clustering of cooperators on the square lattice, while the snapshots for seem to have these feature somewhat less pronounced, although still clearly inferable (note that the distinction of clusters is somewhat difficult due to the continuous array of possible strategies). This suggests that, besides the clustering of cooperators, additional mechanisms may underlie the survival of cooperators at high temptations to defect and within the present setup. The color encoding, as depicted right, indicates the values of for each individual player.

Figure 4. Characteristic spatial distributions of velocities, as obtained for different combinations of and .

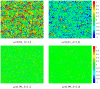
Top row depicts results for , while bottom row features results for . Irrespective of , it can be observed that for the whole population essentially becomes a swarm in that the velocities of all players are much the same and close to zero. The fact that the prevailing velocity is close to zero simply reflects that the stationary state has been reached by means of adaptive, locally-inspired and slow strategy changes (which are, however, very effective even if the temptations to defect are strong). For , however, only isolated clusters can be considered to act as swarms, while the majority of players cannot be associated with any kind of group dynamics and is simply caught in the futile pursuit for the highest, yet for the majority unattainable, payoffs. These results indicate that swarming is an important agonist that promotes cooperation at high temptations to defect (see results presented in Fig. 1). The color encoding, as depicted right, indicates the values of for each individual player, where was chosen sufficiently large such that the stationary state of the game has been reached. Importantly, we note that for the stationary state has in fact been reached, although at a given instance in time the average velocity in the population might be different from zero.