Unraveling gene regulatory networks from time-resolved gene expression data - a measures comparison study
- PMID: 21771321
- PMCID: PMC3161045
- DOI: 10.1186/1471-2105-12-292
Unraveling gene regulatory networks from time-resolved gene expression data - a measures comparison study
Abstract
Background: Inferring regulatory interactions between genes from transcriptomics time-resolved data, yielding reverse engineered gene regulatory networks, is of paramount importance to systems biology and bioinformatics studies. Accurate methods to address this problem can ultimately provide a deeper insight into the complexity, behavior, and functions of the underlying biological systems. However, the large number of interacting genes coupled with short and often noisy time-resolved read-outs of the system renders the reverse engineering a challenging task. Therefore, the development and assessment of methods which are computationally efficient, robust against noise, applicable to short time series data, and preferably capable of reconstructing the directionality of the regulatory interactions remains a pressing research problem with valuable applications.
Results: Here we perform the largest systematic analysis of a set of similarity measures and scoring schemes within the scope of the relevance network approach which are commonly used for gene regulatory network reconstruction from time series data. In addition, we define and analyze several novel measures and schemes which are particularly suitable for short transcriptomics time series. We also compare the considered 21 measures and 6 scoring schemes according to their ability to correctly reconstruct such networks from short time series data by calculating summary statistics based on the corresponding specificity and sensitivity. Our results demonstrate that rank and symbol based measures have the highest performance in inferring regulatory interactions. In addition, the proposed scoring scheme by asymmetric weighting has shown to be valuable in reducing the number of false positive interactions. On the other hand, Granger causality as well as information-theoretic measures, frequently used in inference of regulatory networks, show low performance on the short time series analyzed in this study.
Conclusions: Our study is intended to serve as a guide for choosing a particular combination of similarity measures and scoring schemes suitable for reconstruction of gene regulatory networks from short time series data. We show that further improvement of algorithms for reverse engineering can be obtained if one considers measures that are rooted in the study of symbolic dynamics or ranks, in contrast to the application of common similarity measures which do not consider the temporal character of the employed data. Moreover, we establish that the asymmetric weighting scoring scheme together with symbol based measures (for low noise level) and rank based measures (for high noise level) are the most suitable choices.
Figures

 ,
,  ), where the diagonal of the cross-correlation matrix is set to 0. (b) ROC curves using the ID scoring scheme and different correlation coefficient, such as the simple Pearson correlation coefficient, where the diagonal of cross-correlation matrix is once 0 (μP (diag0)), and another time the diagonal is 1 (μP (diag1)). Furthermore, the ROC curves using the Spearman (μS (diag1)) and the Kendall (μK (diag1)) correlation coefficient, where the diagonal is 1 in both cases, are shown. (c) Evaluation of the ID scoring scheme using information-theoretic measures: simple, conditional and residual mutual information (μI,
), where the diagonal of the cross-correlation matrix is set to 0. (b) ROC curves using the ID scoring scheme and different correlation coefficient, such as the simple Pearson correlation coefficient, where the diagonal of cross-correlation matrix is once 0 (μP (diag0)), and another time the diagonal is 1 (μP (diag1)). Furthermore, the ROC curves using the Spearman (μS (diag1)) and the Kendall (μK (diag1)) correlation coefficient, where the diagonal is 1 in both cases, are shown. (c) Evaluation of the ID scoring scheme using information-theoretic measures: simple, conditional and residual mutual information (μI,  and
and  ). (d) Evaluation of the ID scoring scheme using measures based on symbolic dynamics: symbol sequence similarity (
). (d) Evaluation of the ID scoring scheme using measures based on symbolic dynamics: symbol sequence similarity ( ), the mutual information of the symbol sequences (
), the mutual information of the symbol sequences ( ) and the mean of these both (
) and the mean of these both ( ), as well as the symbol sequence similarity of pairs of time points (
), as well as the symbol sequence similarity of pairs of time points ( (pairs)) and the conditional entropy of the symbols obtained from the pairs of time points (
(pairs)) and the conditional entropy of the symbols obtained from the pairs of time points ( (pairs)). (e) The corresponding ROC curves illustrating the performance of the Time Shift scoring scheme using the Pearson correlation μP, applied in addition to the CLR (measure: μS) and the AWE (measure:
(pairs)). (e) The corresponding ROC curves illustrating the performance of the Time Shift scoring scheme using the Pearson correlation μP, applied in addition to the CLR (measure: μS) and the AWE (measure:  ) scoring scheme. (f) Performance of the AWE algorithm using the selected symbol based measures included in the this study, for example ROC curves for the symbol sequence similarity (
) scoring scheme. (f) Performance of the AWE algorithm using the selected symbol based measures included in the this study, for example ROC curves for the symbol sequence similarity ( ), the mutual information of the symbol sequences (
), the mutual information of the symbol sequences ( ), and the mean of these both (
), and the mean of these both ( ).
).
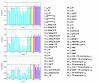
 ), symbol sequence similarity (
), symbol sequence similarity ( ), mutual information of the symbol sequences (
), mutual information of the symbol sequences ( ) and the mean of these two (
) and the mean of these two ( ), and (b) Pearson correlation (μP), partial Pearson correlation (
), and (b) Pearson correlation (μP), partial Pearson correlation ( ), conditional Pearson correlation (
), conditional Pearson correlation ( ), Spearman correlation (μS) and Kendall correlation (μK).
), Spearman correlation (μS) and Kendall correlation (μK).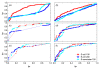
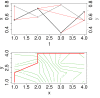
 , (b) conditional Granger causality
, (b) conditional Granger causality  , (c) Spearman correlation μS, (d) simple mutual information μI, (e) symbol sequence similarity
, (c) Spearman correlation μS, (d) simple mutual information μI, (e) symbol sequence similarity  , and (f) residual mutual information
, and (f) residual mutual information  .
.


References
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

