Inferring the structure and dynamics of interactions in schooling fish

Abstract

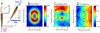
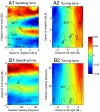
Determining individual-level interactions that govern highly coordinated motion in animal groups or cellular aggregates has been a long-standing challenge, central to understanding the mechanisms and evolution of collective behavior. Numerous models have been proposed, many of which display realistic-looking dynamics, but nonetheless rely on untested assumptions about how individuals integrate information to guide movement. Here we infer behavioral rules directly from experimental data. We begin by analyzing trajectories of golden shiners (Notemigonus crysoleucas) swimming in two-fish and three-fish shoals to map the mean effective forces as a function of fish positions and velocities. Speeding and turning responses are dynamically modulated and clearly delineated. Speed regulation is a dominant component of how fish interact, and changes in speed are transmitted to those both behind and ahead. Alignment emerges from attraction and repulsion, and fish tend to copy directional changes made by those ahead. We find no evidence for explicit matching of body orientation. By comparing data from two-fish and three-fish shoals, we challenge the standard assumption, ubiquitous in physics-inspired models of collective behavior, that individual motion results from averaging responses to each neighbor considered separately; three-body interactions make a substantial contribution to fish dynamics. However, pairwise interactions qualitatively capture the correct spatial interaction structure in small groups, and this structure persists in larger groups of 10 and 30 fish. The interactions revealed here may help account for the rapid changes in speed and direction that enable real animal groups to stay cohesive and amplify important social information.

Fig. 1.

Two-fish configurations. (A) Diagram of dynamical variables. As the fish swim freely in the tank, their bodies form a natural Cartesian coordinate system. We place the focal fish at the origin, pointing north, and measure the relative position and heading of the neighboring fish. The effective force on the focal fish (i.e., its measured acceleration) is decomposed into its speeding and turning components. (B) Probability of finding the neighboring fish at a given position with respect to the focal fish using the framework in A. Each time the neighbor is at a particular position, one count is added to the corresponding bin (see SI Materials and Methods). Contours represent isolevels at 10, 50, and 90% of the “highest” (most visited) bin, which contains 37,481 events. (C and D) Speeding and turning components, respectively, of the mean measured effective force on the focal fish as a function of the neighboring fish’s position. Note that regions of zero effective force correspond to high density regions in B. For all force maps, colors utilize the same scale. For the speeding forces, positive values indicate speeding up and negative values indicate slowing down. For the turning forces, positive values indicate a right turn and negative values indicate a left turn. Distances are expressed in units of body length [BL] and time in seconds [s]. Analysis was restricted to frames in which all fish were at least 2.5 body lengths away from the boundary and moving at a minimum speed of 0.5 [BL/s].

Fig. 2.

Mean measured effective forces as a function of the speed and heading of the neighboring fish. (A1 and A2) Speeding and turning forces as a function of the neighbor’s speed and its front–back or left–right distance, respectively. For a faster-moving neighbor, both measured forces are stronger, and the preferred distance to a neighbor in front becomes larger (the zero-force region in A1 is displaced forward in the front–back axis). (B1 and B2) Speeding and turning forces as a function of the relative heading of the two fish and the front–back or left–right distance, respectively. For the same spatial configuration, the focal fish displays a higher speeding acceleration when both fish are aligned and a higher turning acceleration when they are misaligned. Contours show the probability that fish are in particular configurations, as described in Fig. 1.

Fig. 3.

Nonpairwise interactions in three-fish shoals. (A) Diagram of dynamical variables describing the three-fish configurations. The relative positions of both neighboring fish are expressed in Cartesian coordinates with the focal fish at the origin. Velocities and effective forces are also expressed in the same way as in the two-fish system. For the speeding forces (Top), the positions of both neighbors are projected onto the axis along the focal fish’s direction of motion, and for the turning forces (Bottom), the positions of both neighbors are projected onto the axis perpendicular to the focal fish’s direction of motion. (B1 and B2) Measured speeding and turning forces exerted on the focal fish as a function of the front–back or left–right distances to both neighbors, respectively. Ten-percent contours as described in Fig. 1 are overlaid for reference. (C1 and C2) Predicted speeding and turning forces exerted on the focal fish under the hypothesis that fish average pairwise interactions. The maps show results from averaging the two-fish forces presented in Fig. 1. They are symmetric about the diagonal, because the identities of the two neighbors can be interchanged. Note that they display the same qualitative features as those measured for three-fish shoals (B1 and B2), but with significant residual three-body forces, (D1 and D2). (D1 and D2) Residual speeding and turning forces not accounted for by averaging pairwise responses to neighbors, obtained by subtracting panel C1 from B1 and C2 from B2. The residual forces show a substantial three-body effect producing stronger effective restitution forces (up to 100% stronger in the case of speeding and up to 25% stronger in the case of turning) when the focal fish is between both neighbors. The red patches in D1 occur when one neighbor is close behind and the other is farther ahead, showing a synergistic effect when the focal fish has two independent reasons to accelerate. Similarly, the blue patches occur when one neighbor is just ahead and the other is farther behind, showing a synergistic effect when the focal fish has two independent reasons to decelerate.