Selection of resistant bacteria at very low antibiotic concentrations
- PMID: 21811410
- PMCID: PMC3141051
- DOI: 10.1371/journal.ppat.1002158
Selection of resistant bacteria at very low antibiotic concentrations
Abstract
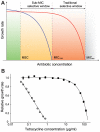
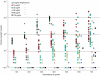
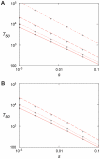
The widespread use of antibiotics is selecting for a variety of resistance mechanisms that seriously challenge our ability to treat bacterial infections. Resistant bacteria can be selected at the high concentrations of antibiotics used therapeutically, but what role the much lower antibiotic concentrations present in many environments plays in selection remains largely unclear. Here we show using highly sensitive competition experiments that selection of resistant bacteria occurs at extremely low antibiotic concentrations. Thus, for three clinically important antibiotics, drug concentrations up to several hundred-fold below the minimal inhibitory concentration of susceptible bacteria could enrich for resistant bacteria, even when present at a very low initial fraction. We also show that de novo mutants can be selected at sub-MIC concentrations of antibiotics, and we provide a mathematical model predicting how rapidly such mutants would take over in a susceptible population. These results add another dimension to the evolution of resistance and suggest that the low antibiotic concentrations found in many natural environments are important for enrichment and maintenance of resistance in bacterial populations.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



Comment in
-
Are subinhibitory concentrations of antibiotics the only culprit of antibiotic resistance?Future Microbiol. 2011 Dec;6(12):1391-4. doi: 10.2217/fmb.11.129. Future Microbiol. 2011. PMID: 22122436
References
-
- Rice LB. The clinical consequences of antimicrobial resistance. Curr Opin Microbiol. 2009;12:476–481. - PubMed
-
- Witte W. Medical consequences of antibiotic use in agriculture. Science. 1998;279:996–997. - PubMed
-
- Aarestrup FM. Veterinary drug usage and antimicrobial resistance in bacteria of animal origin. Basic Clin Pharmacol. 2005;96:271–281. - PubMed
-
- Martinez JL. Antibiotics and antibiotic resistance genes in natural environments. Science. 2008;321:365–367. - PubMed
-
- Ferber D. Superbugs on the hoof? Science. 2000;288:792–794. - PubMed
Publication types
MeSH terms
Substances
Associated data
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
- Actions
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

