Models of place and grid cell firing and theta rhythmicity
- PMID: 21820895
- PMCID: PMC3223517
- DOI: 10.1016/j.conb.2011.07.002
Models of place and grid cell firing and theta rhythmicity
Abstract
Neuronal firing in the hippocampal formation (HF) of freely moving rodents shows striking examples of spatialorganization in the form of place, directional, boundary vector and grid cells. The firing of place and grid cells shows an intriguing form of temporal organization known as 'theta phase precession'. We review the mechanisms underlying theta phase precession of place cell firing, ranging from membrane potential oscillations to recurrent connectivity, and the relevant intra-cellular and extra-cellular data. We then consider the use of these models to explain the spatial structure of grid cell firing, and review the relevant intra-cellular and extra-cellular data. Finally, we consider the likely interaction between place cells, grid cells and boundary vector cells in estimating self-location as a compromise between path-integration and environmental information.
Copyright © 2011 Elsevier Ltd. All rights reserved.
Figures


References
-
- Vanderwolf CH. Hippocampal electrical activity and voluntary movement in the rat. Electroencephalogr.Clin.Neurophysiol. 1969;26:407–418. - PubMed
-
- O’Keefe J. Place units in the hippocampus of the freely moving rat. Exp.Neurol. 1976;51:78–109. - PubMed
-
- O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. - PubMed
-
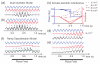
•• The phase of place cell firing relative to the theta rhythm in freely moving rats relfects the location of the animal. Suggests that this results from the summation of two theta-band oscillations with slightly different frequencies (the dual oscillator model).
-
- Jensen O, Lisman JE. Position reconstruction from an ensemble of hippocampal place cells: contribution of theta phase coding. J.Neurophysiol. 2000;83:2602–2609. - PubMed
-
- Huxter J, Burgess N, O’Keefe J. Independent rate and temporal coding in hippocampal pyramidal cells. Nature. 2003;425:828–832. - PMC - PubMed
-
• The rate of firing and the theta-phase of firing of place cells can vary independently, potentially encoding different types of information simultaneously using rate and phase codes.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

