Quantifying negative feedback regulation by micro-RNAs
- PMID: 21832809
- PMCID: PMC3184398
- DOI: 10.1088/1478-3975/8/5/055002
Quantifying negative feedback regulation by micro-RNAs
Abstract
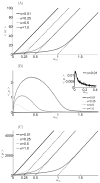
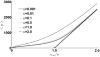
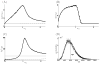
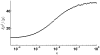
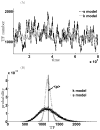
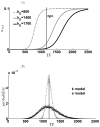
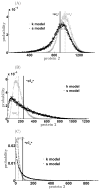
Micro-RNAs (miRNAs) play a crucial role in post-transcriptional gene regulation by pairing with target mRNAs to repress protein production. It has been shown that over one-third of human genes are targeted by miRNA. Although hundreds of miRNAs have been identified in mammalian genomes, the function of miRNA-based repression in the context of gene regulation networks still remains unclear. In this study, we explore the functional roles of feedback regulation by miRNAs. In a model where repression of translation occurs by sequestration of mRNA by miRNA, we find that miRNA and mRNA levels are anti-correlated, resulting in larger fluctuation in protein levels than theoretically expected assuming no correlation between miRNA and mRNA levels. If miRNA repression is due to a catalytic suppression of translation rates, we analytically show that the protein fluctuations can be strongly repressed with miRNA regulation. We also discuss how either of these modes may be relevant for cell function.
Figures

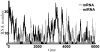



Similar articles
-
Inter- and intra-combinatorial regulation by transcription factors and microRNAs.BMC Genomics. 2007 Oct 30;8:396. doi: 10.1186/1471-2164-8-396. BMC Genomics. 2007. PMID: 17971223 Free PMC article.
-
Regulation of mRNA translation and stability by microRNAs.Annu Rev Biochem. 2010;79:351-79. doi: 10.1146/annurev-biochem-060308-103103. Annu Rev Biochem. 2010. PMID: 20533884 Review.
-
Effects of microRNA-mediated negative feedback on gene expression noise.Biophys J. 2023 Nov 7;122(21):4220-4240. doi: 10.1016/j.bpj.2023.09.019. Epub 2023 Oct 6. Biophys J. 2023. PMID: 37803829 Free PMC article.
-
MicroRNAs reinforce repression of PRC2 transcriptional targets independently and through a feed-forward regulatory network.Genome Res. 2019 Feb;29(2):184-192. doi: 10.1101/gr.238311.118. Epub 2019 Jan 16. Genome Res. 2019. PMID: 30651280 Free PMC article.
-
IsomiRs: Expanding the miRNA repression toolbox beyond the seed.Biochim Biophys Acta Gene Regul Mech. 2020 Apr;1863(4):194373. doi: 10.1016/j.bbagrm.2019.03.005. Epub 2019 Apr 4. Biochim Biophys Acta Gene Regul Mech. 2020. PMID: 30953728 Free PMC article. Review.
Cited by
-
Functional characteristics of a double negative feedback loop mediated by microRNAs.Cogn Neurodyn. 2013 Oct;7(5):417-29. doi: 10.1007/s11571-012-9236-7. Epub 2013 Jan 5. Cogn Neurodyn. 2013. PMID: 24427216 Free PMC article.
-
Serum microRNA-185 Levels and Myocardial Injury in Patients with Acute ST-segment Elevation Myocardial Infarction.Intern Med. 2022 Jan 15;61(2):151-158. doi: 10.2169/internalmedicine.7594-21. Epub 2021 Jul 10. Intern Med. 2022. PMID: 34248121 Free PMC article.
-
Understanding microRNA-mediated gene regulatory networks through mathematical modelling.Nucleic Acids Res. 2016 Jul 27;44(13):6019-35. doi: 10.1093/nar/gkw550. Epub 2016 Jun 17. Nucleic Acids Res. 2016. PMID: 27317695 Free PMC article.
-
OncomiRdbB: a comprehensive database of microRNAs and their targets in breast cancer.BMC Bioinformatics. 2014 Jan 15;15:15. doi: 10.1186/1471-2105-15-15. BMC Bioinformatics. 2014. PMID: 24428888 Free PMC article.
-
Massive computational acceleration by using neural networks to emulate mechanism-based biological models.Nat Commun. 2019 Sep 25;10(1):4354. doi: 10.1038/s41467-019-12342-y. Nat Commun. 2019. PMID: 31554788 Free PMC article.
References
-
- Bartel David P. Micrornas: genomics, biogenesis, mechanism, and function. Cell. 2004 Jan;116(2):281–297. - PubMed
-
- Lewis Benjamin P, Burge Christopher B, Bartel David P. Conserved seed pairing, often flanked by adenosines, indicates that thousands of human genes are microrna targets. Cell. 2005 Jan;120(1):15–20. - PubMed
-
- Cohen Stephen M, Brennecke Julius, Stark Alexander. Denoising feedback loops by thresholding–a new role for micrornas. Genes Dev. 2006 Oct;20(20):2769–2772. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
