Fitness costs and diversity of the cytotoxic T lymphocyte (CTL) response determine the rate of CTL escape during acute and chronic phases of HIV infection
- PMID: 21835793
- PMCID: PMC3187476
- DOI: 10.1128/JVI.00655-11
Fitness costs and diversity of the cytotoxic T lymphocyte (CTL) response determine the rate of CTL escape during acute and chronic phases of HIV infection
Abstract
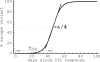
HIV-1 often evades cytotoxic T cell (CTL) responses by generating variants that are not recognized by CTLs. We used single-genome amplification and sequencing of complete HIV genomes to identify longitudinal changes in the transmitted/founder virus from the establishment of infection to the viral set point at 1 year after the infection. We found that the rate of viral escape from CTL responses in a given patient decreases dramatically from acute infection to the viral set point. Using a novel mathematical model that tracks the dynamics of viral escape at multiple epitopes, we show that a number of factors could potentially contribute to a slower escape in the chronic phase of infection, such as a decreased magnitude of epitope-specific CTL responses, an increased fitness cost of escape mutations, or an increased diversity of the CTL response. In the model, an increase in the number of epitope-specific CTL responses can reduce the rate of viral escape from a given epitope-specific CTL response, particularly if CD8+ T cells compete for killing of infected cells or control virus replication nonlytically. Our mathematical framework of viral escape from multiple CTL responses can be used to predict the breadth and magnitude of HIV-specific CTL responses that need to be induced by vaccination to reduce (or even prevent) viral escape following HIV infection.
Figures
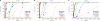
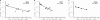
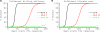


References
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Research Materials

