Inference for discretely observed stochastic kinetic networks with applications to epidemic modeling

Abstract

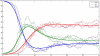
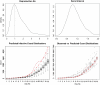
We present a new method for Bayesian Markov Chain Monte Carlo-based inference in certain types of stochastic models, suitable for modeling noisy epidemic data. We apply the so-called uniformization representation of a Markov process, in order to efficiently generate appropriate conditional distributions in the Gibbs sampler algorithm. The approach is shown to work well in various data-poor settings, that is, when only partial information about the epidemic process is available, as illustrated on the synthetic data from SIR-type epidemics and the Center for Disease Control and Prevention data from the onset of the H1N1 pandemic in the United States.

Fig. 1.

ODE and SKN trajectories for SIRS model species (susceptibles, infectives, and removed, respectively, top, middle, and bottom curve at the origin) with total population size M = 100.

Fig. 2.

Datapoints along the trajectories for susceptibles, infectives, and removed (top, middle, and bottom curve at the origin, respectively) in the SIRS model. Vertical lines indicate the data batches used for the 3 first dense grid scenarios (m = 1) reported on in Table 1. Circled values mark the data set used in fourth (sparse grid) scenario when m = 3.

Fig. 3.

Results of the H1N1 model analysis. Top panel left: the posterior distribution of the reproduction number R₀ = θ₁/θ₂. Top panel right: the posterior distribution of θ₃ or the rate of conversion from “latent” to “symptomatic” infectives (the serial interval). Bottom panel left: model predicted posterior cross-sectional distributions of the time-specific counts of “latent” infectives (bar plots) along with observed and smoothed counts (bullets) of H1N1 cases in the continental United States during the onset of the epidemic. Bottom panel right: goodness of fit analysis. The comparison of the observed data with the model predicted 95% posterior credibility bounds (dashed lines) along with the cross-sectional distributions of the observed counts generated from the model with estimated parameters.