Communication: Iteration-free, weighted histogram analysis method in terms of intensive variables

Abstract

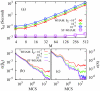
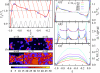
We present an iteration-free weighted histogram method in terms of intensive variables that directly determines the inverse statistical temperature, β(S) = ∂S/∂E, with S the microcanonical entropy. The method eliminates iterative evaluations of the partition functions intrinsic to the conventional approach and leads to a dramatic acceleration of the posterior analysis of combining statistically independent simulations with no loss in accuracy. The synergistic combination of the method with generalized ensemble weights provides insights into the nature of the underlying phase transitions via signatures in β(S) characteristic of finite size systems. The versatility and accuracy of the method is illustrated for the Ising and Potts models.

Figure 1

ST-WHAM results for the 2D Ising model with linear dimension L = 32 and M = 4. (a) H^ex (solid line), $H_{\alpha }^{\mathrm{ex}}$ (dashed line), and $f_{\alpha }^{*}=H_{\alpha }^{\mathrm{ex}}∕H^{\mathrm{ex}}$ (dotted line); (b) ${\beta }_S^{*}$ (solid line) and ${\overline{\beta }}_{\alpha }^S$ (dashed line); (c) β_H (solid line) and ${\overline{\beta }}_{\alpha }^H$ (dashed line), and (d) β_W (solid line) and ${\overline{\beta }}_{\alpha }^W$ (dashed line) as a function of e = E/2L². The magnitude of $H_{\alpha }^{\mathrm{ex}}$ is adjusted for visualization, and α = 1, 2, 3, and 4 from left to right in (a). The same color scheme is used for all figures.

Figure 2

(a) Time τ_M required to compute S given $H_{\alpha }^{\mathrm{ex}}$ at M equally distributed temperatures between T₁ = 2.0 and T_M = 2.6 for L = 32, (b) the error estimates ε(β_S), and (c) ε(S) as a function of Monte Carlo steps per spin (MCS) averaged over ten realizations of canonical runs with M = 4.

Figure 3

Results for the q-state 2D Potts model. (a) $T_{\alpha }^{\mathrm{eff}}$ (dashed line), $T_S^{*}$ (solid line), H_α (dotted line), and characteristic energies ${\tilde{e}}_{\mathrm{o}}$, ${\tilde{e}}_{\mathrm{s},1}$, ${\tilde{e}}_{\mathrm{ds},2}$, ${\tilde{e}}_{\mathrm{ds},1}$, ${\tilde{e}}_{\mathrm{s},2}$, and ${\tilde{e}}_{\mathrm{d}}$ (see the text) from left to right (circles); (b) representative configurations at different α for q = 50 and L = 24, (c) $T_S^{*}\left(\tilde{e}\right)$, (d) ${{\beta }_S^{*}}^{\prime }$ for L = 24 (solid line) and L = 36 (dashed line); (e) free energy densities per spin $F(\tilde{e},T_c)$ with varying q. In (a), α = 10, 20, 30, 40, 50, 60, 70, 80, and 90 in both $T_{\alpha }^{\mathrm{eff}}$ and H_α. The same color scheme is applied to (c)–(e).