Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments

Abstract

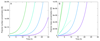
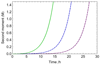
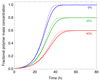
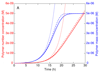
Self-assembly processes resulting in linear structures are often observed in molecular biology, and include the formation of functional filaments such as actin and tubulin, as well as generally dysfunctional ones such as amyloid aggregates. Although the basic kinetic equations describing these phenomena are well-established, it has proved to be challenging, due to their non-linear nature, to derive solutions to these equations except for special cases. The availability of general analytical solutions provides a route for determining the rates of molecular level processes from the analysis of macroscopic experimental measurements of the growth kinetics, in addition to the phenomenological parameters, such as lag times and maximal growth rates that are already obtainable from standard fitting procedures. We describe here an analytical approach based on fixed-point analysis, which provides self-consistent solutions for the growth of filamentous structures that can, in addition to elongation, undergo internal fracturing and monomer-dependent nucleation as mechanisms for generating new free ends acting as growth sites. Our results generalise the analytical expression for sigmoidal growth kinetics from the Oosawa theory for nucleated polymerisation to the case of fragmenting filaments. We determine the corresponding growth laws in closed form and derive from first principles a number of relationships which have been empirically established for the kinetics of the self-assembly of amyloid fibrils.

Fig. 1

Schema illustrating the microscopic processes of polymerisation with secondary pathways treated in this paper. Primary nucleation (a) leads to the creation of a polymer of length n_c from soluble monomer. Filaments grow linearly (b) from both ends in a reversible manner with monomers also able to dissociate from the ends (c). The secondary pathways (d) and (e) lead to the creation of of new fibril ends from pre-existing polymers; fragmentation (d) is discussed in the first part of this paper, and monomer-dependent secondary nucleation (e) is discussed in the second part.

Fig. 2

Growth kinetics in the early time limit with different initial seed concentrations (from left to right): M(0) = 6.25 · 10⁻⁷. M(0) = 1.25 · 10⁻⁷M, M(0) = 2.5 · 10⁻⁸M, M(0) = 5 · 10⁻⁹, The other parameters are: k_off = 0, P(0) = M(0)/5000, k₊ = 5 · 10⁴ M⁻¹ s⁻¹, k_off = 0, k₋ = 10⁻⁹ s⁻¹ k_n = 0, m_tot = 5 · 10⁻⁵M. In (A) is P(t) the zeroth moment of the distribution f(t, j) given by Eq. (28) and in (B) is M(t) the first moment from Eq. (27). The dashed lines in (B) show the initial rate dM/dt|_t=0 = 2k₊m_totP|_t=0.

Fig. 3

Time evolution of the second moment Q(t) of the length distribution in the early time limit for differing primary nucleation rates (from left to right): k_n = 2 · 10⁻³ M⁻¹ s⁻¹, k_n = 2 · 10⁻⁴ M⁻¹ s⁻¹, k_n = 2 · 10⁻⁵ M⁻¹ s⁻¹. The other parameters are: k₊ = 5 · 10⁴ M⁻¹ s⁻¹, k_off = 0, k₋ = 2 · 10⁻⁸ s⁻¹, m_tot = 5 · 10⁻⁶ M, n_c = 2, M(0) = P(0) = 0. The dashed lines show the analytical result Eq. (34) derived by neglecting the third central moment. The solid lines show the numerical result from the master equation, Eq. (2), which accounts for all central moments.

Fig. 4

Kinetics of fibrillar growth. Growth through nucleation, elongation and fragmentation leads to sigmoidal kinetic curves for the mass concentration of fibrils as a function of time. Solid line: first moment M(t) computed from the numerical solution of the master equation Eq. (2). Dashed curve: analytical solution given in Eq. (39). Dotted curve: early time limit from Eq. (28). The parameters are: k₊ = 5 · 10⁴ M⁻¹ s⁻¹, k_off = 0, k₋ = 2 · 10⁻⁸ s⁻¹, m_tot = 5 · 10⁻⁶ M, k_n = 2 · 10⁻⁵ M⁻¹ s⁻¹, n_c = 2, M(0) = P(0) = 0. Panel (B) shows the maximal growth rate r_max, polymer concentration corresponding to the maximal growth rate M_max, time of maximal growth rate t_max and lag time τ_lag.

Fig. 5

Effect of the depolymerisation rate. Sigmoids for increasing depolymerisation rates are shown. Depolymerisation rates are given as a percentage of k₊m_tot. In most cases of practical interest [36, 58], k_off ≪ k₊m_tot. Solid lines: first moment M(t) computed from the numerical solution of the master equation Eq. (2). Dashed lines: analytical solution given in Eq. (39). The parameters are: k₊ = 5 · 10⁴ M⁻¹ s⁻¹, k₋ = 2 · 10⁻⁸ s⁻¹, m_tot = 1 · 10⁻⁶ M, k_n = 5 · 10⁻⁵ M⁻¹ s⁻¹, n_c = 2, M(0) = 1 · 10⁻⁸ M, P(0) = M(0)/5000.

Fig. 6

Low breakage rate limit, k₋ → 0. Panel A shows Eq. (39) evaluated for successively smaller breakage rates k₋ = 10⁻⁷ s⁻¹ k₋ = 10⁻⁸ s⁻¹ k₋ = 10⁻⁹ s⁻¹ k₋ = 10⁻¹⁰ s⁻¹. The other parameters are k₊ = 5 · 10⁴ M⁻¹ s⁻¹, k_off = 0, m_tot = 50 · 10⁻⁶ M, k_n = 10⁻⁶ M⁻¹ s⁻¹, M(0) = P(0) = 0. Panel (B) shows an expanded portion of the t → 0 limit showing the progressive transition from exponential to polynomial growth (red line, shows Eq. (52)) as a function of time when nucleation takes over from breakage as the most important source of new fibril ends.

Fig. 7

Effect of elongation rate and breakage rate on the growth kinetics in the absence of nucleation. In A the elongation rate k₊ is varied, from left to right: k₊ = 7.3 · 10⁵ M⁻¹ s⁻¹, k₊ = 2.9 · 10⁵ M⁻¹ s⁻¹, k₊ = 1.2 · 10⁵ M⁻¹ s⁻¹, k₊ = 4.7 · 10⁴ M⁻¹ s⁻¹, k₊ = 1.9 · 10⁴ M⁻¹ s⁻¹ and k₊ = 7.5 · 10³ M⁻¹ s⁻¹ and the other parameters are k_off = 0, k_n = 0, k₋ = 10⁻⁹ s⁻¹, m_tot = 50 µM M(0) = 1 nM and P(0) = M(0)/1000. In B the breakage rate is varied from left to right: k₋ = 6.4 · 10⁻⁸ s⁻¹, k₋ = 3.2 · 10⁻⁸ s⁻¹, k₋ = 1.6 · 10⁻⁸ s⁻¹, k₋ = 8.0 · 10⁻⁹ s⁻¹, k₋ = 4.0 · 10⁻⁹ s⁻¹ and k₋ = 2.0 · 10⁻⁹ s⁻¹ and the other parameters are: k_off = 0, k_n = 0, k₊ = 1 · 10⁻⁴ M⁻¹ s⁻¹, m_tot = 50 µM M(0) = 1 nM and P(0) = M(0)/1000.

Fig. 8

Effect of monomer concentration on the growth kinetics in the absence of nucleation. A: Polymer mass concentration M(t) Eq. (39) as a function of time for different total monomer concentrations, from left to right: m_tot = 20 µM, m_tot = 40 µM, m_tot = 80 µM, m_tot = 160 µM, m_tot = 320 µM and m_tot = 640 µM. The values used for the other parameters are:k_off = 0, k_n = 0, k₊ = 2 · 10⁴ s⁻¹ M⁻¹, k₋ = 10⁻⁹ s⁻¹, M(0) = 100 nM, P(0) = M(0)/1000. In B are shown the normalised polymer mass fractions M(t)/m_tot as a function of time, for the same monomer concentrations as in A.

Fig. 9

Polymer number concentration. The time evolution of the polymer number concentration P (red) from Eq. (56) and mass concentration M (blue) from Fig. 4 are shown for the same parameter values as in Fig. 4. The solid lines show the numerical results, the dashed lines are the analytical solutions and the dotted lines are early time limits from Eqs. (27) and (28).

Fig. 10

Time evolution of the central moments of the filament length distribution. Panel A shows the mean filament length computed numerically (solid black line) and a comparison to the early time linear solution Eq. (58) (dotted blue line) and the full closed-form solution Eq. (61) (dashed blue line). The standard deviation of the length distribution is shown in B. The black line is the result from evaluating the standard deviation from a numerical solution to the master equation Eq. (2), the blue dotted line shows the linear solution valid for early times Eq. (63) and the dashed line shows the approximation V (t) ~ L(t) valid for late times Eq. (64).

Fig. 11

Effect of initial seed concentration. A: Polymer mass concentration M(t) Eq. (39) as a function of time for different initial seed concentrations, from left to right: M(0) = 729 nM. M(0) = 243 nM, M(0) = 81 nM, M(0) = 27 nM, M(0) = 9 nM and M(0) = 3 nM, The values used for the other parameters are: k_off = 0, k_n = 0, k₊ = 5·10⁴ s⁻¹ M⁻¹, k₋ = 10⁻⁹ s⁻¹, m_tot = 50 µM and P(0) = M(0)/1000. Panel B shows the growth rate dM(t)/dt. Interestingly the maximal growth rate is independent of the seed concentration, except for seed concentrations that are higher than the critical concentration (M_c = 260 nM for the parameters used) as described in the text. The maximal growth rate Eq. (78) (1.3 · 10⁻⁹ for the parameters used) is shown as a dashed red line.

Fig. 12

Nucleated growth with varying monomer concentrations. A: Polymer mass concentration M(t) Eq. (39) as a function of time for different total monomer concentrations, from left to right: m_tot = 1.3 · 10⁻⁴ M, m_tot = 6.4 · 10⁻⁵ M, m_tot = 3.2 · 10⁻⁵ M, m_tot = 1.6 · 10⁻⁵ M, m_tot = 8.0 · 10⁻⁶ M, m_tot = 4.0 · 10⁻⁶ M. The values used for the other parameters are: k_off = 0, n_c = 2, k_n = 10⁻⁸ M⁻¹ s⁻¹, k₊ = 5 · 10⁴ s⁻¹ M⁻¹, k₋ = 5 · 10⁻⁸ s⁻¹, M(0) = P(0) = 0. In B are shown the normalised polymer mass fractions M(t)/m_tot as a function of time, for the same monomer concentrations as in A.