Computability, Gödel's incompleteness theorem, and an inherent limit on the predictability of evolution
- PMID: 21849390
- PMCID: PMC3284140
- DOI: 10.1098/rsif.2011.0479
Computability, Gödel's incompleteness theorem, and an inherent limit on the predictability of evolution
Abstract
The process of evolutionary diversification unfolds in a vast genotypic space of potential outcomes. During the past century, there have been remarkable advances in the development of theory for this diversification, and the theory's success rests, in part, on the scope of its applicability. A great deal of this theory focuses on a relatively small subset of the space of potential genotypes, chosen largely based on historical or contemporary patterns, and then predicts the evolutionary dynamics within this pre-defined set. To what extent can such an approach be pushed to a broader perspective that accounts for the potential open-endedness of evolutionary diversification? There have been a number of significant theoretical developments along these lines but the question of how far such theory can be pushed has not been addressed. Here a theorem is proven demonstrating that, because of the digital nature of inheritance, there are inherent limits on the kinds of questions that can be answered using such an approach. In particular, even in extremely simple evolutionary systems, a complete theory accounting for the potential open-endedness of evolution is unattainable unless evolution is progressive. The theorem is closely related to Gödel's incompleteness theorem, and to the halting problem from computability theory.
Figures
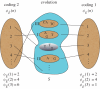
 , over the first three time steps. If evolution is progressive, then coding 2 is possible, and the theorem then says that we can ‘decide’ any population state, s ∈ S. For example, we can decide state ‘T,T,T’ by finding its code (i.e. ‘1’), and then iterating the map,
, over the first three time steps. If evolution is progressive, then coding 2 is possible, and the theorem then says that we can ‘decide’ any population state, s ∈ S. For example, we can decide state ‘T,T,T’ by finding its code (i.e. ‘1’), and then iterating the map,  , until we obtain an output greater than ‘1’ (this occurs at time step 1 because
, until we obtain an output greater than ‘1’ (this occurs at time step 1 because  ). If ‘1’ has not yet been visited by this time, it never will be. Conversely, if all population states are decidable, then, under coding 1, we can apply the algorithm provided in part 2 of the theorem's proof to obtain coding 2, thereby demonstrating that evolution is progressive.
). If ‘1’ has not yet been visited by this time, it never will be. Conversely, if all population states are decidable, then, under coding 1, we can apply the algorithm provided in part 2 of the theorem's proof to obtain coding 2, thereby demonstrating that evolution is progressive.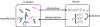
References
-
- Yedid G., Bell G. 2002. Macroevolution simulated with autonomously replicating computer programs. Nature 420, 810–81210.1038/nature01151 (doi:10.1038/nature01151) - DOI - DOI - PubMed
-
- Levinton J. 1988. Genetics, paleontology and macroevolution. Cambridge, UK: Cambridge University Press
-
- Fontana W., Buss L. 1994. The arrival of the fittest: towards a theory of biological organization. Bull. Math. Biol. 56, 1–64
-
- Wagner G. P., Altenberg L. 1996. Perspective: complex adaptations and the evolution of evolvability. Evolution 50, 967–97610.2307/2410639 (doi:10.2307/2410639) - DOI - DOI - PubMed
-
- DeVries H. 1904. Species and varieties: their origin by mutation. Chicago, IL: Open Court
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

