What does physics have to do with cancer?
- PMID: 21850037
- PMCID: PMC3711102
- DOI: 10.1038/nrc3092
What does physics have to do with cancer?
Abstract
Large-scale cancer genomics, proteomics and RNA-sequencing efforts are currently mapping in fine detail the genetic and biochemical alterations that occur in cancer. However, it is becoming clear that it is difficult to integrate and interpret these data and to translate them into treatments. This difficulty is compounded by the recognition that cancer cells evolve, and that initiation, progression and metastasis are influenced by a wide variety of factors. To help tackle this challenge, the US National Cancer Institute Physical Sciences-Oncology Centers initiative is bringing together physicists, cancer biologists, chemists, mathematicians and engineers. How are we beginning to address cancer from the perspective of the physical sciences?
Conflict of interest statement
The authors declare no competing financial interests.
Figures
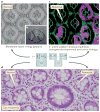
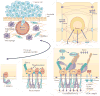

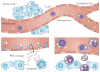
References
-
- Paget S. The distribution of secondary growths in cancer of the breast. Lancet. 1889;1:571–573. - PubMed
-
- Boehm T, Folkman J, Browder T, O’Reilly MS. Antiangiogenic therapy of experimental cancer does not induce acquired drug resistance. Nature. 1997;390:404–407. - PubMed
-
- Nowell PC. The clonal evolution of tumor cell populations. Science. 1976;194:23–28. - PubMed
-
- Fisher JC. Multiple-mutation theory of carcinogenesis. Nature. 1958;181:651–652. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

