Cell receptor and surface ligand density effects on dynamic states of adhering circulating tumor cells

Abstract

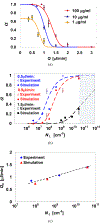
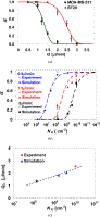
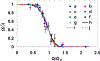
Dynamic states of cancer cells moving under shear flow in an antibody-functionalized microchannel are investigated experimentally and theoretically. The cell motion is analyzed with the aid of a simplified physical model featuring a receptor-coated rigid sphere moving above a solid surface with immobilized ligands. The motion of the sphere is described by the Langevin equation accounting for the hydrodynamic loadings, gravitational force, receptor-ligand bindings, and thermal fluctuations; the receptor-ligand bonds are modeled as linear springs. Depending on the applied shear flow rate, three dynamic states of cell motion have been identified: (i) free motion, (ii) rolling adhesion, and (iii) firm adhesion. Of particular interest is the fraction of captured circulating tumor cells, defined as the capture ratio, via specific receptor-ligand bonds. The cell capture ratio decreases with increasing shear flow rate with a characteristic rate. Based on both experimental and theoretical results, the characteristic flow rate increases monotonically with increasing either cell-receptor or surface-ligand density within certain ranges. Utilizing it as a scaling parameter, flow-rate dependent capture ratios for various cell-surface combinations collapse onto a single curve described by an exponential formula.

Fig. 1

(a) A side-view image of a typical CTC on a solid surface with approximately a spherical shape, and (b) An illustration of the physical model for the theoretical analysis; the cell is represented as a rigid sphere, with receptors on its surface, moving under linear shear flow above a surface immobilized with ligands; receptor-ligand bonds are modeled as linear springs.

Fig. 2

Measured and calculated capture ratio of EpCAM-expressing MDA-MB-231 cells in anti-EpCAM functionalized microchannels as a function of the applied shear flow rate. The predicted capture ratio is calculated based on the velocity of 50 cells averaged over a 60s time period under each flow rate assuming: h=490nm, K=850nN/m, N_R=1.35×10⁸/cm², and D=0.05μm. The three characteristic dynamic states observed under certain flow rate ranges are marked by the shaded regions.

Fig. 3

(a) Cell-surface gap estimate based on matching simulated gap-size dependent hydrodynamic velocity (solid lines) with average cell velocity measured under various flow rates (dash lines); the average free-motion velocity was measured for MDA-MB-231 cells passing through anti-N-cadherin functionalized microchannels with negligible receptor-ligand interaction, and (b) Spring constant estimate based on matching calculated spring-constant dependent cell velocity with measured cell velocity during capture; the firm-adhesion velocity was measured for MDA-MB-231 cells captured in anti-EpCAM functionalized microchannels under a flow rate of 0.9μl/min. The cell-surface gap is estimated to be about h=490nm, independent of the applied flow rate, while the spring constant is estimated to be about K=850nN/m assuming D=0.05μm and N_R=1.35×10⁸/cm² in the calculations.

Fig. 4

Simulated time evolution of the velocity of several cells under flow-rate dependent dynamic states of: (a) firm adhesion (Q=0.9 μl/min), (b) rolling adhesion (Q=1.5 μl/min), and (c) free motion (Q=3 μl/min). The numerical computations were carried out for: h = 490 nm, K = 850 nN/m, N_R = 1.35×10⁸/cm², and D = 0.05 μm (corresponding to the motion of MDA-MB-231 cells on an anti-EpCAM functionalized surface.)

Fig. 5

(a) Capture ratio measurements (symbols) and predictions based on Equation 4 (curves) of MDA-MB-231 cells as a function of the applied flow rate in microchannels functionalized with EpCAM antibodies at various concentrations; measured and predicted effect of surface-ligand density on: (b) MDA-MB-231 cell capture ratio under three selected flow rates, and (c) characteristic flow rate for the capture of MDA-MB-231 cells, with N_R=1.35×10⁸/cm², in anti-EpCAM functionalized microchannels.

Fig. 6

(a) Capture ratio measurements (symbols) and predictions based on Equation 4 (curves) of MDA-MB-231 and BT-20 cells, varying in EpCAM receptor density, as a function of the flow rate in microchannels functionalized with EpCAM antibodies at a concentration of 100μg/ml; measured and predicted effect of cell-receptor density on: (b) MDA-MB-231 and BT-20 capture ratio under selected flow rates, and (c) characteristic flow rate for capturing MDA-MB-231 and BT-20 cells in anti-EpCAM functionalized microchannels with N_L=4.0×10¹⁰/cm².

Fig. 7

All measured and simulated normalized capture ratios as a function of the normalized flow rate collapse onto a single exponential function presented in Equation 4. Experimental data sets ‘a’, ‘b’, and ‘c’ are for MDA-MB-231 cells in a channel coated with EpCAM antibodies at concentrations of 100, 10, and 1μg/ml, respectively, while ‘d’ is for BT-20 cells in a channel coated with EpCAM antibodies at a concentration of 100μg/ml; data sets ‘e’, ‘f’ and ‘g’ are calculations for cell receptor densities of 5.4×10⁸, 6.4×10⁹ and 1.6×10¹⁰/cm², respectively, with ligand density of 4.0×10¹⁰/cm²; and curves ‘h’, ‘i’ and ‘j’ are exponential functions with exponents B=6±1.