Protein-coat dynamics and cluster phases in intracellular trafficking
- PMID: 21862842
- PMCID: PMC3393765
- DOI: 10.1088/0953-8984/23/37/374105
Protein-coat dynamics and cluster phases in intracellular trafficking
Abstract
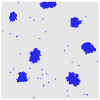
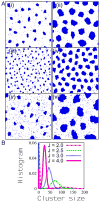
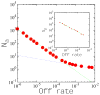
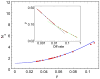
Clustering of membrane proteins is a hallmark of biological membranes' lateral organization and crucial to their function. However, the physical properties of these protein aggregates remain poorly understood. Ensembles of coat proteins, the example considered here, are necessary for intracellular transport in eukaryotic cells. Assembly and disassembly rates for coat proteins involved in intracellular vesicular trafficking must be carefully controlled: their assembly deforms the membrane patch and drives vesicle formation, yet the protein coat must rapidly disassemble after vesiculation. Motivated by recent experimental findings for protein-coat dynamics, we study a dynamical Ising-type model for coat assembly and disassembly, and demonstrate how simple dynamical rules generate a robust, steady-state distribution of protein clusters (corresponding to intermediate budded shapes) and how cluster sizes are controlled by the kinetics. We interpret the results in terms of both vesiculation and the coupling to cargo proteins.
Figures
Similar articles
-
COPII coat assembly and selective export from the endoplasmic reticulum.J Biochem. 2004 Dec;136(6):755-60. doi: 10.1093/jb/mvh184. J Biochem. 2004. PMID: 15671485 Review.
-
COP sets TRAPP for vesicles.Dev Cell. 2007 Mar;12(3):326-7. doi: 10.1016/j.devcel.2007.02.001. Dev Cell. 2007. PMID: 17336899
-
Vesicle-mediated export from the ER: COPII coat function and regulation.Biochim Biophys Acta. 2013 Nov;1833(11):2464-72. doi: 10.1016/j.bbamcr.2013.02.003. Epub 2013 Feb 15. Biochim Biophys Acta. 2013. PMID: 23419775 Free PMC article. Review.
-
Generation of nonidentical compartments in vesicular transport systems.J Cell Biol. 2005 Jan 17;168(2):271-80. doi: 10.1083/jcb.200409087. J Cell Biol. 2005. PMID: 15657397 Free PMC article.
-
The COPII cage: unifying principles of vesicle coat assembly.Nat Rev Mol Cell Biol. 2006 Oct;7(10):727-38. doi: 10.1038/nrm2025. Nat Rev Mol Cell Biol. 2006. PMID: 16990852 Review.
References
-
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. Garland Science; New York, NY: 2008.
-
- Stradner A, Sedgwick H, Cardinaux F, Poon WCK, Egelhaaf SU, Schurtenberger P. Nature. 2004;432:492. - PubMed
-
- Louis AA, Allahyarov E, Lowen H, Roth R. Phys Rev E. 2002;65:061407. - PubMed
-
- Likos CN. Phys Rep. 2002;348:267.
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
