A new model for the estimation of cell proliferation dynamics using CFSE data

Abstract

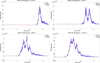
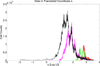
CFSE analysis of a proliferating cell population is a popular tool for the study of cell division and divisionlinked changes in cell behavior. Recently Banks et al. (2011), Luzyanina et al. (2009), Luzyanina et al. (2007), a partial differential equation (PDE) model to describe lymphocyte dynamics in a CFSE proliferation assay was proposed. We present a significant revision of this model which improves the physiological understanding of several parameters. Namely, the parameter used previously as a heuristic explanation for the dilution of CFSE dye by cell division is replaced with a more physical component, cellular autofluorescence. The rate at which label decays is also quantified using a Gompertz decay process. We then demonstrate a revised method of fitting the model to the commonly used histogram representation of the data. It is shown that these improvements result in a model with a strong physiological basis which is fully capable of replicating the behavior observed in the data.

Figure 1

Original histogram data from [13, 45].

Figure 2

Total label content ∫ zn(t, z)dz over time for the data from [13]. The increase at t = 72 hours is a physiological impossibility.

Figure 3

Results of fitting the exponential model (5) and the Gompertz model (6) to the mean CFSE data. For both Donor 1 (top) and Donor 2 (bottom), we see that the Gompertz model is more capable of accurately replicating the observed data.

Figure 4

OLS best-fit solution with α = α(y) (13 nodes), β = β(y) (5 nodes). 21 total parameters in the model, total cost J(θ̂_OLS) = 1.7270 × 10¹². While the model clearly is not accurate in allowing far too many cells with large division number too early in time, the locations of the division peaks along the horizontal axis are quite accurate, in support of the role of autofluorescence as well as the Gompertz decay of label.

Figure 5

OLS best-fit solution with α = α(t, s), β = β(s). 73 total parameters in the model, total cost J(θ̂_OLS) = 3.0901 × 10¹¹.

Figure 6

Data for t = 24, 48, 96, 120, respectively, plotted in the translated coordinate s. Observe that the peaks corresponding to distinct division numbers closely align.

Figure 7

Average proliferation rate as a function of time for each generation of cells.

Figure 8

Left: Estimated proliferation rate function for three difference choices of nodes. Top: 7 nodes evenly spaced in [1.125,2.925]. Middle: 13 nodes evenly spaced in [1.125,2.925]. Bottom: 25 nodes evenly spaced in [1.125,2.925]. Note that, while the overall shape of α(y) remains largely the same, the middle figure seems to provide the most information while remaining some semblance of regularity. These functions can be used to determine the average rate of proliferation in terms of the number of divisions undergone (Table 2). It is these computed average rates of proliferation that are of biological interest, and these rates are consistently estimated regardless of the parameterization used. Right: the corresponding estimated death rate function β(y), estimated using 5 fixed nodes in each case.

Figure 9

OLS best-fit solution with α = α(t, y), β = β(y). 73 total parameters in the model, total cost J(θ̂_OLS) = 3.1302 × 10¹¹. The use of a time-dependent proliferation rate results in a significant improvement in the fit of the model to the data.

Figure 10

OLS best-fit proliferation and death rate function α(s, t) (top) and β(s) (bottom), respectively, when the proliferation rate is assumed to depend on both s and t. The parameterization in terms of s, a coordinate which correlates very strongly with division number, reduces the possibility of error or bias when average proliferation rates (in terms of division number) are computed (Figure 7).