Phylogenetic and epidemic modeling of rapidly evolving infectious diseases

Abstract

Epidemic modeling of infectious diseases has a long history in both theoretical and empirical research. However the recent explosion of genetic data has revealed the rapid rate of evolution that many populations of infectious agents undergo and has underscored the need to consider both evolutionary and ecological processes on the same time scale. Mathematical epidemiology has applied dynamical models to study infectious epidemics, but these models have tended not to exploit--or take into account--evolutionary changes and their effect on the ecological processes and population dynamics of the infectious agent. On the other hand, statistical phylogenetics has increasingly been applied to the study of infectious agents. This approach is based on phylogenetics, molecular clocks, genealogy-based population genetics and phylogeography. Bayesian Markov chain Monte Carlo and related computational tools have been the primary source of advances in these statistical phylogenetic approaches. Recently the first tentative steps have been taken to reconcile these two theoretical approaches. We survey the Bayesian phylogenetic approach to epidemic modeling of infection diseases and describe the contrasts it provides to mathematical epidemiology as well as emphasize the significance of the future unification of these two fields.

Fig. 1

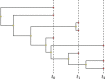
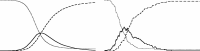
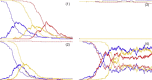
A serially sampled time tree of a rapidly evolving virus, showing that the sampling time interval [t₀,t₂] represents a substantial fraction of the time back to the common ancestor. Red circles represent sampled viruses (three viruses sampled at each of three times) and yellow circles represent hypothetical common ancestors. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2

Three time-trees estimated using BEAST. Notice the different orders of magnitude of time spanned and the different proportion of the tree spanned by samples. (a) A phylogeny of Hepatitis C spanning all major genotypes: the sampling interval spans 32 years [1977, 2009] but represents a very small fraction of the estimated root height (≈0.019t_MRCA), and this root height estimate could be severely underestimated and very misleading. (b) A phylogeny of HIV-1 M group: the sampling interval spans 27 years [1978, 2005] and represents a significant fraction (≈0.32t_MRCA) of the overall tree height, but still small enough that the estimated root should be viewed with caution. (c) A phylogeny of human Influenza A subtype H3N2: the sampling interval spans 12.2 years [1993.1, 2005.3] and represents almost the full height of the tree (≈0.94t_MRCA), and all divergence times are likely to be quite accurately estimated, since interpolation between many known sample times is inherently less error prone than extrapolation to ancient divergence times.

Fig. 3

The underlying Wright–Fisher population and serially-sampled genealogies from two populations. The first population has a constant population size over the history of the genealogy, while the second population has been exponentially growing. The coalescent likelihood calculates the probability of a genealogy given a particular background population history (e.g., constant or exponentially growing) and can therefore be employed to estimate the population history that best reflects the shape of the co-estimated phylogeny.

Fig. 4

Realization of an SIR model showing the dynamics of susceptible (dotted line), infected (solid line) and recovered (dashed line) individuals over time. The stochastic version leads to less “smooth” dynamics (right hand side).

Fig. 5

Realization of a stochastic SIR model in a structured population. Simulated viral dynamics in n = 3 subpopulations, each color denoting one of them. The numbers of susceptibles (dotted lines) are plotted against the numbers of infected individuals (solid lines), a full infection tree and three sample trees at different times throughout the epidemic.

Fig. 6

Simulated viral outbreak under stochastic SIR (1–3) and SIS (4) model among three populations (denoted by blue, yellow and red curves). The initial condition is a single infected individual in the blue population. In (3) the disease does not break out (numbers of susceptibles in dotted lines and infected in solid lines). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)