A Micromechanics Finite-Strain Constitutive Model of Fibrous Tissue

Abstract

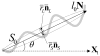
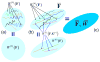
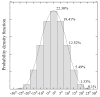
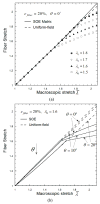
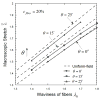
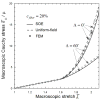
Biological tissues have unique mechanical properties due to the wavy fibrous collagen and elastin microstructure. In inflation, a vessel easily distends under low pressure but becomes stiffer when the fibers are straightened to take up the load. The current microstructural models of blood vessels assume affine deformation; i.e., the deformation of each fiber is assumed to be identical to the macroscopic deformation of the tissue. This uniform-field (UF) assumption leads to the macroscopic (or effective) strain energy of the tissue that is the volumetric sum of the contributions of the tissue components. Here, a micromechanics-based constitutive model of fibrous tissue is developed to remove the affine assumption and to take into consideration the heterogeneous interactions between the fibers and the ground substance. The development is based on the framework of a recently developed second-order homogenization theory, and takes into account the waviness, orientations, and spatial distribution of the fibers, as well as the material nonlinearity at finite-strain deformation. In an illustrative simulation, the predictions of the macroscopic stress-strain relation, and the statistical deformation of the fibers are compared to the UF model, as well as finite-element (FE) simulation. Our predictions agree well with the FE results, while the UF predictions significantly overestimate. The effects of fiber distribution and waviness on the macroscopic stress-strain relation are also investigated. The present mathematical model may serves as a foundation for native as well as for engineered tissues and biomaterials.

Figure 1

The geometry of an undulated collagen fiber with total length S₀ and straight length l₀. The overall fiber direction is N, which is described by the overall orientation angle θ for 2-D problem. The undeformed cross-sectional area is described by the long axis r̄_L/n̄_L and short axis r̄_Sn̄_S.

Figure 2

Conceptual demonstration of homogenization method. (a) A representative volume element of a fibrous tissue at reference state. All the fibers are undulated and exhibit the same property as the matrix with strain energy function (SEF) W₀; (b) When subjected to a macroscopic F̄, some fibers are straightened and show stiffer property with SEF W ^(r) as in Eq. (2b). (c) The effectively homogeneous material with macroscopic SEF W̄.

Figure 3

Discretization of the Beta-distribution of fiber orientation θ. The corresponding cumulative probability D(x) is given for each region. The span of Beta-distribution is Δ = 60°, and α = β = 6. The continuous cumulative probability D(x) is discretized by rounding method: D(x)= p(x+ h/2) − p(x−h/2), in which h is interval between regions.

Figure 4

The macroscopic strain energy function (a) and Cauchy stress-stretch relation (b) of fibrous tissue with 20% randomly distributed collagen fibers. Values are normalized with material parameter μ. The reference fiber material has waviness λ₀ =1.6.

Figure 5

The influence of waviness λ₀ and orientation angle θ on the statistical average microscopic stretch of the fibers. (a) The microscopic stretch of matrix phase (solid line) and collagen fibers (symbols) with waviness λ₀ = 1.5, 1.6, 1.7 and 1.8, and orientation angle θ= 0°, while the uniform-field prediction (dashed line) is independent of the waviness; (b) The microscopic stretch of collagen fibers with orientation angle θ= 0°, 10° and 20°, and waviness λ₀ =1.6.

Figure 6

The macroscopic stretch that straightens the undulated collagen fibers with orientation angle θ= 0°, 15° and 25°. The uniform-field predictions (dashed line) are consistently higher than SOE predictions (symbols).

Figure 7

The macroscopic tensile stress-strain curve of fibrous tissues with 20% randomly distributed collagen fibers. The Beta-distribution of the fiber orientation angle θ has mean M= 0° and span Δ= 0° and 60°, respectively. All the fibers are assumed to have the same waviness λ₀ =1.6.