Coarse-to-fine changes of receptive fields in lateral geniculate nucleus have a transient and a sustained component that depend on distinct mechanisms
- PMID: 21931739
- PMCID: PMC3170358
- DOI: 10.1371/journal.pone.0024523
Coarse-to-fine changes of receptive fields in lateral geniculate nucleus have a transient and a sustained component that depend on distinct mechanisms
Abstract
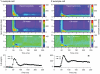
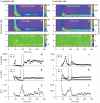
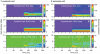
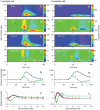
Visual processing in the brain seems to provide fast but coarse information before information about fine details. Such dynamics occur also in single neurons at several levels of the visual system. In the dorsal lateral geniculate nucleus (LGN), neurons have a receptive field (RF) with antagonistic center-surround organization, and temporal changes in center-surround organization are generally assumed to be due to a time-lag of the surround activity relative to center activity. Spatial resolution may be measured as the inverse of center size, and in LGN neurons RF-center width changes during static stimulation with durations in the range of normal fixation periods (250-500 ms) between saccadic eye-movements. The RF-center is initially large, but rapidly shrinks during the first ~100 ms to a rather sustained size. We studied such dynamics in anesthetized cats during presentation (250 ms) of static spots centered on the RF with main focus on the transition from the first transient and highly dynamic component to the second more sustained component. The results suggest that the two components depend on different neuronal mechanisms that operate in parallel and with partial temporal overlap rather than on a continuously changing center-surround balance. Results from mathematical modeling further supported this conclusion. We found that existing models for the spatiotemporal RF of LGN neurons failed to account for our experimental results. The modeling demonstrated that a new model, in which the response is given by a sum of an early transient component and a partially overlapping sustained component, adequately accounts for our experimental data.
Conflict of interest statement
Figures



Similar articles
-
Dynamics of spatial resolution of single units in the lateral geniculate nucleus of cat during brief visual stimulation.J Neurophysiol. 2007 Feb;97(2):1445-56. doi: 10.1152/jn.01338.2005. Epub 2006 Aug 16. J Neurophysiol. 2007. PMID: 16914606
-
Temporally advanced dynamic change of receptive field of lateral geniculate neurons during brief visual stimulation: Effects of brainstem peribrachial stimulation.Neuroscience. 2013 Jul 9;242:85-96. doi: 10.1016/j.neuroscience.2013.03.037. Epub 2013 Mar 29. Neuroscience. 2013. PMID: 23542736
-
Mapping the primate lateral geniculate nucleus: a review of experiments and methods.J Physiol Paris. 2014 Feb;108(1):3-10. doi: 10.1016/j.jphysparis.2013.10.001. Epub 2013 Nov 21. J Physiol Paris. 2014. PMID: 24270042 Free PMC article. Review.
-
Dynamic spatial processing originates in early visual pathways.J Neurosci. 2006 Nov 8;26(45):11763-74. doi: 10.1523/JNEUROSCI.3297-06.2006. J Neurosci. 2006. PMID: 17093097 Free PMC article.
-
Binocular response modulation in the lateral geniculate nucleus.J Comp Neurol. 2019 Feb 15;527(3):522-534. doi: 10.1002/cne.24417. Epub 2018 Mar 9. J Comp Neurol. 2019. PMID: 29473163 Free PMC article. Review.
Cited by
-
Population receptive field models capture the event-related magnetoencephalography response with millisecond resolution.Imaging Neurosci (Camb). 2024 Sep 18;2:imag-2-00285. doi: 10.1162/imag_a_00285. eCollection 2024. Imaging Neurosci (Camb). 2024. PMID: 40800296 Free PMC article.
-
Biophysical Network Modelling of the dLGN Circuit: Different Effects of Triadic and Axonal Inhibition on Visual Responses of Relay Cells.PLoS Comput Biol. 2016 May 20;12(5):e1004929. doi: 10.1371/journal.pcbi.1004929. eCollection 2016 May. PLoS Comput Biol. 2016. PMID: 27203421 Free PMC article.
-
Layer 3 Dynamically Coordinates Columnar Activity According to Spatial Context.J Neurosci. 2019 Jan 9;39(2):281-294. doi: 10.1523/JNEUROSCI.1568-18.2018. Epub 2018 Nov 20. J Neurosci. 2019. PMID: 30459226 Free PMC article.
-
Biophysical network modeling of the dLGN circuit: Effects of cortical feedback on spatial response properties of relay cells.PLoS Comput Biol. 2018 Jan 29;14(1):e1005930. doi: 10.1371/journal.pcbi.1005930. eCollection 2018 Jan. PLoS Comput Biol. 2018. PMID: 29377888 Free PMC article.
-
Firing-rate based network modeling of the dLGN circuit: Effects of cortical feedback on spatiotemporal response properties of relay cells.PLoS Comput Biol. 2018 May 17;14(5):e1006156. doi: 10.1371/journal.pcbi.1006156. eCollection 2018 May. PLoS Comput Biol. 2018. PMID: 29771919 Free PMC article.
References
-
- Breitmeyer BG. Simple reaction time as a measure of the temporal response properties of transient and sustained channels. Vision Res. 1975;15:1411–1412. - PubMed
-
- Marr D, Poggio T. A computational theory of human stereo vision. Proc R Soc Lond B Biol Sci. 1979;204:301–328. - PubMed
-
- Ringach DL, Hawken MJ, Shapley R. Dynamics of orientation tuning in macaque primary visual cortex. Nature. 1997;387:281–284. - PubMed
-
- Menz MD, Freeman RD. Stereoscopic depth processing in the visual cortex: a coarse-to-fine mechanism. Nat Neurosci. 2003;6:59–65. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

