An exact expression to calculate the derivatives of position-dependent observables in molecular simulations with flexible constraints
- PMID: 21931757
- PMCID: PMC3171457
- DOI: 10.1371/journal.pone.0024563
An exact expression to calculate the derivatives of position-dependent observables in molecular simulations with flexible constraints
Erratum in
-
Correction: An Exact Expression to Calculate the Derivatives of Position-Dependent Observables in Molecular Simulations with Flexible Constraints.PLoS One. 2017 Dec 6;12(12):e0189454. doi: 10.1371/journal.pone.0189454. eCollection 2017. PLoS One. 2017. PMID: 29211794 Free PMC article.
Abstract
In this work, we introduce an algorithm to compute the derivatives of physical observables along the constrained subspace when flexible constraints are imposed on the system (i.e., constraints in which the constrained coordinates are fixed to configuration-dependent values). The presented scheme is exact, it does not contain any tunable parameter, and it only requires the calculation and inversion of a sub-block of the Hessian matrix of second derivatives of the function through which the constraints are defined. We also present a practical application to the case in which the sought observables are the Euclidean coordinates of complex molecular systems, and the function whose minimization defines the flexible constraints is the potential energy. Finally, and in order to validate the method, which, as far as we are aware, is the first of its kind in the literature, we compare it to the natural and straightforward finite-differences approach in a toy system and in three molecules of biological relevance: methanol, N-methyl-acetamide and a tri-glycine peptide.
Conflict of interest statement
Figures
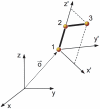

 , associated to atom
, associated to atom  , and the unitary vector
, and the unitary vector  corresponding to the direction around which all atoms
corresponding to the direction around which all atoms  with chains
with chains  containing
containing  rotate if
rotate if  is varied while the rest of internal coordinates are kept constant.
is varied while the rest of internal coordinates are kept constant.
 , associated to atom
, associated to atom  . The positive sense of rotation is indicated in the figure, and we can distinguish between two situations regarding covalent connectivity: a) principal dihedral angle, and b) phase dihedral angle (see ref. [37]).
. The positive sense of rotation is indicated in the figure, and we can distinguish between two situations regarding covalent connectivity: a) principal dihedral angle, and b) phase dihedral angle (see ref. [37]).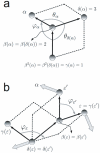
 connecting
connecting  to atom 1, but that are nevertheless used to position
to atom 1, but that are nevertheless used to position  .
.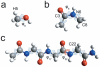
 are indicated with light-blue arrows, and some internal coordinates and some atoms that appear in the discussion are specifically labeled. The constrained dihedral angle
are indicated with light-blue arrows, and some internal coordinates and some atoms that appear in the discussion are specifically labeled. The constrained dihedral angle  is indicated by a red arrow in GLY3.
is indicated by a red arrow in GLY3.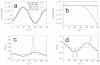
 coordinate of atom 5 in methanol, (b) the bond length
coordinate of atom 5 in methanol, (b) the bond length  associated to it, (c) the bond angle
associated to it, (c) the bond angle  , and (d) the dihedral angle
, and (d) the dihedral angle  as a function of the unconstrained coordinate
as a function of the unconstrained coordinate  . Both the results of the new algorithm and those obtained by finite differences (FD) are depicted. The key for the different types of line is the same in the four graphs.
. Both the results of the new algorithm and those obtained by finite differences (FD) are depicted. The key for the different types of line is the same in the four graphs.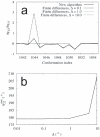
 of the constrained dihedral angle
of the constrained dihedral angle  , describing a peptide bond rotation in GLY3, with respect to the unconstrained coordinate
, describing a peptide bond rotation in GLY3, with respect to the unconstrained coordinate  for a selected set of conformations in the working set. (b) Minimum-energy value of the constrained dihedral angle
for a selected set of conformations in the working set. (b) Minimum-energy value of the constrained dihedral angle  in the conformation 1044 of GLY3 for different values of the displacement
in the conformation 1044 of GLY3 for different values of the displacement  in the unconstrained coordinate
in the unconstrained coordinate  .
.
 (see the text for a more precise definition). (a) Error averaged to all conformations and all atoms of the three molecular systems studied. (b) Error averaged to all conformations of the
(see the text for a more precise definition). (a) Error averaged to all conformations and all atoms of the three molecular systems studied. (b) Error averaged to all conformations of the  -coordinate of three particular
-coordinate of three particular  -row atoms in NMA.
-row atoms in NMA.
 and
and  corresponds to the one explored in this work. Contour level lines and colour level indication in the surface have been added for visual comfort. All units are arbitrary.
corresponds to the one explored in this work. Contour level lines and colour level indication in the surface have been added for visual comfort. All units are arbitrary.References
-
- Rapaport DC. Cambridge University Press, 2nd edition; 2004. The art of molecular dynamics simulation.
-
- Allen MP, Tildesley DJ. Oxford: Clarendon Press; 2005. Computer simulation of liquids.
-
- Frenkel D, Smit B. Orlando FL: Academic Press, 2nd edition; 2002. Understanding molecular simulations: From algorithms to applications.
-
- Car R, Parrinello M. Unified approach for molecular dynamics and density-functional theory. Phys Rev Lett. 1985;55:2471–2474. - PubMed
-
- Hutter J, Curioni A. Car-Parrinello molecular dynamics on massively parallel computers. ChemPhysChem. 2005;6:1788–1793. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

