Accounting for diffusion in agent based models of reaction-diffusion systems with application to cytoskeletal diffusion

Abstract

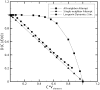
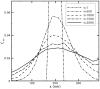
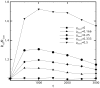
Diffusion plays a key role in many biochemical reaction systems seen in nature. Scenarios where diffusion behavior is critical can be seen in the cell and subcellular compartments where molecular crowding limits the interaction between particles. We investigate the application of a computational method for modeling the diffusion of molecules and macromolecules in three-dimensional solutions using agent based modeling. This method allows for realistic modeling of a system of particles with different properties such as size, diffusion coefficients, and affinity as well as the environment properties such as viscosity and geometry. Simulations using these movement probabilities yield behavior that mimics natural diffusion. Using this modeling framework, we simulate the effects of molecular crowding on effective diffusion and have validated the results of our model using Langevin dynamics simulations and note that they are in good agreement with previous experimental data. Furthermore, we investigate an extension of this framework where single discrete cells can contain multiple particles of varying size in an effort to highlight errors that can arise from discretization that lead to the unnatural behavior of particles undergoing diffusion. Subsequently, we explore various algorithms that differ in how they handle the movement of multiple particles per cell and suggest an algorithm that properly accommodates multiple particles of various sizes per cell that can replicate the natural behavior of these particles diffusing. Finally, we use the present modeling framework to investigate the effect of structural geometry on the directionality of diffusion in the cell cytoskeleton with the observation that parallel orientation in the structural geometry of actin filaments of filopodia and the branched structure of lamellipodia can give directionality to diffusion at the filopodia-lamellipodia interface.

Figure 1. Comparison of algorithms for diffusion in crowded environments.

Effective diffusion coefficient at low time scales versus normalized free particle concentration (volume density) for two agent based model algorithms and a Langevin dynamics simulation for comparison. The graph shows the single-neighbor attempt algorithm to best represent diffusion at higher concentrations as the effective diffusion of this algorithm decreases linearly with increased concentration as does the Langevin dynamics model. As the graph shows, the single-neighbor attempt and Langevin dynamics simulation exhibit the same negative linear slope with a slight difference in offsets resulting from the different definition of particle volume between the two modeling techniques. Higher concentration data points for Langevin dynamics have been omitted as the volume definition of particles leads to volume overlap at this concentration.

Figure 2. Natural log of anomalous diffusion of the Single-Neighbor attempt is in agreement with experimental data.

Natural log of effective anomalous diffusion coefficient versus normalized free particle concentration (volume density) for two agent based model algorithms. The linear relationship between natural log of the anomalous diffusion coefficient and concentration in the single-neighbor attempt algorithm is in good agreement with experimental data for protein self diffusion .

Figure 3. Algorithms for multi-particle per cell diffusion.

Flowcharts showing the algorithm of three various methods for simulating steric repulsion of multiple particles per cell. a) the Volume Limit (VL) method is the most computationally efficient, b) followed by the Reduced Probability + Volume Limit (RP + VL) method and c) the Reduced Probability (RP) method being the least computationally efficient. The degree of accuracy for which each method models steric repulsion is illustrated in Fig. 4.

Figure 4. Comparison of the validity of multi-particle per cell diffusion algorithms.

In systems of high concentration a) 500 particles in a system with 1000 cells, b) 1000 particles in a system with 1000 cells and c) 2000 particles in a system with 1000 cells, it can be seen that three different methods for handling the movement of multiple particles per cell result in significantly different behavior. The volume limit method (VL) is the most computationally efficient by simply limiting the movement of particles that would result in the fraction of occupied volume of a cell exceeding 1. However, it is also the least accurate when dealing with crowded environments. The combined reduced probability and volume limit method (RP + VL) is slightly less computationally efficient but is much more representative of crowded diffusion when the particles are of smaller volume. The reduced probability method (RP) is the least computationally efficient of the three but best represents the crowded diffusion for most particle sizes. Additionally, the system with 500 particles in 1000 cells deviates the least from actual when using the RP method while the more crowded systems deviate more, confirming that the RP method can accurately model physiologically relevant concentrations.

Figure 5. Representative cross-sectional illustration of simulation environment.

Representatitve cross-sectional illustration of the xy-plane of the three dimensional simulation box of size L_X = 400 nm, L_Y = 200 nm, and L_Z = 100 nm with periodic boundary conditions in the y-direction only. The parallel filaments in the right half of the box (x>200 nm) represent the filopodia while filaments in the left half (x<200 nm) represent the lamellipodia in the cell. The green particles represent the freely diffusing actin monomers which are distributed in three dimensional space near x = 200 nm.

Figure 6. Density of diffusing actin monomers as a function of time and position.

Normalized free particle concentration as a function of position for snapshots of time ranging from 1 to 2000 time steps with a time step increment of 74 µs for a fixed actin filament volume density of 0.25 averaged over ten runs. Initially at t = 1 the distribution of particles is uniform whereas at each subsequent time step shown, the filopodia region (x>200nm) is seen to have a higher free particle concentration than the lamellipodia region (x<200nm).

Figure 7. Directionality of actin monomer diffusion as a function of time and concentration.

Ratio between the center of mass of particles diffused in the filopodia to that of the lamellipodia as a function of time for different fixed actin filament volume densities. There is a tendency for particles to diffuse towards the filopodia region as a result of the geometry of filaments in each region. This phenomenon is only amplified as the density of fixed actin filaments is increased.

Figure 8. Illustration of movement probabilities in a single dimension.

Discretized one-dimensional space with square lattices of length ΔL depicting how probabilities of particles existing in a cell at time t combined with movement probabilities result in a change in the probability of a particle occupying a cell at time t+Δt as outlined by Eq. 7. Note that the circles in each cell do not represent individual particles; rather they qualitatively represent probabilities of a particle residing in that cell.

Figure 9. Model validation process.

Method for modeling diffusion using physically observed diffusion coefficients (translated to movement probabilities) as an input in an agent based model. Additional details regarding the movement algorithm (specifically the single-neighbor attempt) are illustrated.

Figure 10. Comparison of computational costs between agent based and Langevin dynamics methods.

Benchmark showing compute time between a Langevin dynamics simulation and an agent based model of 400 particles diffusing in the same size simulation box and both simulations having the same fraction of volume occupied. The agent based model used a discretized simulation box of 13×13×13 with cubic cells of 4 nm in length. The Langevin dynamics model incorporated the Cichocki and Hinsen method for simulating hard-spheres and utilized further optimizations such as neighbor lists to maximize computational efficiency. *The Langevin dynamics simulation cutoff was set lower than typical to simulate hard spheres to match that of the agent based model. Typical Langevin dynamics models use higher cutoffs resulting in additional computation time.