Mercedes-Benz water molecules near hydrophobic wall: integral equation theories vs Monte Carlo simulations
- PMID: 21992334
- PMCID: PMC3206897
- DOI: 10.1063/1.3644934
Mercedes-Benz water molecules near hydrophobic wall: integral equation theories vs Monte Carlo simulations
Abstract
Associative version of Henderson-Abraham-Barker theory is applied for the study of Mercedes-Benz model of water near hydrophobic surface. We calculated density profiles and adsorption coefficients using Percus-Yevick and soft mean spherical associative approximations. The results are compared with Monte Carlo simulation data. It is shown that at higher temperatures both approximations satisfactory reproduce the simulation data. For lower temperatures, soft mean spherical approximation gives good agreement at low and at high densities while in at mid range densities, the prediction is only qualitative. The formation of a depletion layer between water and hydrophobic surface was also demonstrated and studied.
© 2011 American Institute of Physics
Figures


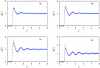
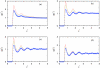




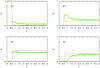

Similar articles
-
Theory for the three-dimensional Mercedes-Benz model of water.J Chem Phys. 2009 Nov 21;131(19):194504. doi: 10.1063/1.3259970. J Chem Phys. 2009. PMID: 19929057 Free PMC article.
-
The application of the integral equation theory to study the hydrophobic interaction.J Chem Phys. 2014 Jan 14;140(2):024502. doi: 10.1063/1.4858398. J Chem Phys. 2014. PMID: 24437891 Free PMC article.
-
The application of the thermodynamic perturbation theory to study the hydrophobic hydration.J Chem Phys. 2013 Jul 14;139(2):024101. doi: 10.1063/1.4812744. J Chem Phys. 2013. PMID: 23862923 Free PMC article.
-
Voids, generic van der Waals equation of state, and transport coefficients of liquids.Phys Chem Chem Phys. 2007 Dec 21;9(47):6171-86. doi: 10.1039/b705542k. Epub 2007 Jul 24. Phys Chem Chem Phys. 2007. PMID: 18046466 Review.
-
Recent developments in quantum Monte Carlo simulations with applications for cold gases.Rep Prog Phys. 2012 Sep;75(9):094501. doi: 10.1088/0034-4885/75/9/094501. Epub 2012 Aug 10. Rep Prog Phys. 2012. PMID: 22885729 Review.
Cited by
-
Two dimensional fluid with one site-site associating point. Monte Carlo, integral equation and thermodynamic perturbation theory study.J Mol Liq. 2018 Nov 15;270:87-96. doi: 10.1016/j.molliq.2017.12.111. Epub 2017 Dec 27. J Mol Liq. 2018. PMID: 30546180 Free PMC article.
-
A Simple Two Dimensional Model of Methanol.J Mol Liq. 2018 Jul 15;262:46-57. doi: 10.1016/j.molliq.2018.04.055. Epub 2018 Apr 13. J Mol Liq. 2018. PMID: 30364695 Free PMC article.
-
Integral equation and thermodynamic perturbation theory for a two-dimensional model of chain-forming fluid.J Mol Liq. 2017 Jul;238:129-135. doi: 10.1016/j.molliq.2017.04.095. Epub 2017 Apr 21. J Mol Liq. 2017. PMID: 28729752 Free PMC article.
-
Statistical-mechanical liquid theories reproduce anomalous thermodynamic properties of explicit two-dimensional water models.Phys Rev E. 2022 Sep;106(3-1):034115. doi: 10.1103/PhysRevE.106.034115. Phys Rev E. 2022. PMID: 36266898 Free PMC article.
-
Isothermal-isobaric algorithm to study the effects of rotational degrees of freedom-Benz water model.J Mol Liq. 2022 Mar 1;349:118152. doi: 10.1016/j.molliq.2021.118152. Epub 2021 Nov 23. J Mol Liq. 2022. PMID: 37727581 Free PMC article.
References
-
- Torrie G. M., Kusalik P. G., and Patey G. N., J. Chem. Phys. 88, 7826 (1988).10.1063/1.454296 - DOI
-
- Torrie G. M. and Patey G. N., J. Chem. Phys. 97, 12909 (1993).10.1021/j100151a045 - DOI
-
- Kinoshita M. and Harada M., Mol. Phys. 81, 1473 (1994).10.1080/00268979400101011 - DOI
-
- Kinoshita M., Condens. Matter Phys. 10, 387 (2007).
-
- Kinoshita M. and Hirata F., J. Chem. Phys. 104, 8807 (1996).10.1063/1.471570 - DOI
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

