Pupil Dilation Signals Surprise: Evidence for Noradrenaline's Role in Decision Making
- PMID: 21994487
- PMCID: PMC3183372
- DOI: 10.3389/fnins.2011.00115
Pupil Dilation Signals Surprise: Evidence for Noradrenaline's Role in Decision Making
Abstract
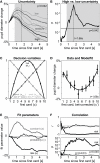
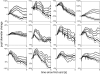
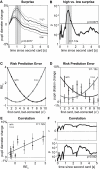
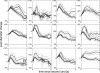
Our decisions are guided by the rewards we expect. These expectations are often based on incomplete knowledge and are thus subject to uncertainty. While the neurophysiology of expected rewards is well understood, less is known about the physiology of uncertainty. We hypothesize that uncertainty, or more specifically errors in judging uncertainty, are reflected in pupil dilation, a marker that has frequently been associated with decision making, but so far has remained largely elusive to quantitative models. To test this hypothesis, we measure pupil dilation while observers perform an auditory gambling task. This task dissociates two key decision variables - uncertainty and reward - and their errors from each other and from the act of the decision itself. We first demonstrate that the pupil does not signal expected reward or uncertainty per se, but instead signals surprise, that is, errors in judging uncertainty. While this general finding is independent of the precise quantification of these decision variables, we then analyze this effect with respect to a specific mathematical model of uncertainty and surprise, namely risk and risk prediction error. Using this quantification, we find that pupil dilation and risk prediction error are indeed highly correlated. Under the assumption of a tight link between noradrenaline (NA) and pupil size under constant illumination, our data may be interpreted as empirical evidence for the hypothesis that NA plays a similar role for uncertainty as dopamine does for reward, namely the encoding of error signals.
Keywords: human; noradrenaline; psychophysics; pupil; surprise; uncertainty.
Figures

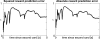
References
-
- Astafiev S. V., Snyder A. Z., Shulman G. L., Corbetta M. (2010). Comment on “Modafinil shifts human locus coeruleus to low-tonic, high-phasic activity during functional MRI” and “homeostatic sleep pressure and responses to sustained attention in the suprachiasmatic area.” Science 328, 309. - PMC - PubMed
-
- Benjamini Y., Hochberg Y. (1995). Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. Series B Stat. Methodol. 57, 289–300
LinkOut - more resources
Full Text Sources

