A multi-cell, multi-scale model of vertebrate segmentation and somite formation
- PMID: 21998560
- PMCID: PMC3188485
- DOI: 10.1371/journal.pcbi.1002155
A multi-cell, multi-scale model of vertebrate segmentation and somite formation
Abstract
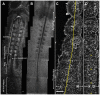
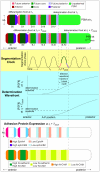
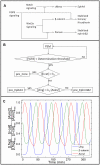
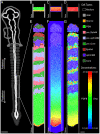
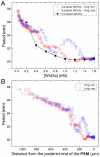
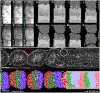
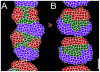
Somitogenesis, the formation of the body's primary segmental structure common to all vertebrate development, requires coordination between biological mechanisms at several scales. Explaining how these mechanisms interact across scales and how events are coordinated in space and time is necessary for a complete understanding of somitogenesis and its evolutionary flexibility. So far, mechanisms of somitogenesis have been studied independently. To test the consistency, integrability and combined explanatory power of current prevailing hypotheses, we built an integrated clock-and-wavefront model including submodels of the intracellular segmentation clock, intercellular segmentation-clock coupling via Delta/Notch signaling, an FGF8 determination front, delayed differentiation, clock-wavefront readout, and differential-cell-cell-adhesion-driven cell sorting. We identify inconsistencies between existing submodels and gaps in the current understanding of somitogenesis mechanisms, and propose novel submodels and extensions of existing submodels where necessary. For reasonable initial conditions, 2D simulations of our model robustly generate spatially and temporally regular somites, realistic dynamic morphologies and spontaneous emergence of anterior-traveling stripes of Lfng. We show that these traveling stripes are pseudo-waves rather than true propagating waves. Our model is flexible enough to generate interspecies-like variation in somite size in response to changes in the PSM growth rate and segmentation-clock period, and in the number and width of Lfng stripes in response to changes in the PSM growth rate, segmentation-clock period and PSM length.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures




References
-
- Gossler A, Hrabe de Angelis M. Somitogenesis. Curr Top Dev Biol. 1998;38:225–287. - PubMed
-
- Kulesa PM, Fraser SE. Cell dynamics during somite boundary formation revealed by time-lapse analysis. Science. 2002;298:991–995. - PubMed
-
- Dequeant ML, Glynn E, Gaudenz K, Wahl M, Chen J, et al. A complex oscillating network of signaling genes underlies the mouse segmentation clock. Science. 2006;314:1595–1598. - PubMed
-
- Wahl MB, Deng C, Lewandoski M, Pourquie O. FGF signaling acts upstream of the NOTCH and WNT signaling pathways to control segmentation clock oscillations in mouse somitogenesis. Development. 2007;134:4033–4041. - PubMed
-
- Lewis J. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr Biol. 2003;13:1398–1408. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

