A malaria transmission-directed model of mosquito life cycle and ecology

Abstract

Background: Malaria is a major public health issue in much of the world, and the mosquito vectors which drive transmission are key targets for interventions. Mathematical models for planning malaria eradication benefit from detailed representations of local mosquito populations, their natural dynamics and their response to campaign pressures.

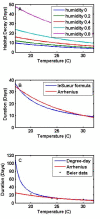
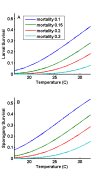
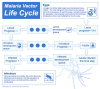
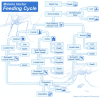
Methods: A new model is presented for mosquito population dynamics, effects of weather, and impacts of multiple simultaneous interventions. This model is then embedded in a large-scale individual-based simulation and results for local elimination of malaria are discussed. Mosquito population behaviours, such as anthropophily and indoor feeding, are included to study their effect upon the efficacy of vector control-based elimination campaigns.

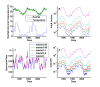
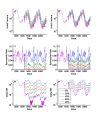
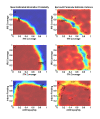
Results: Results for vector control tools, such as bed nets, indoor spraying, larval control and space spraying, both alone and in combination, are displayed for a single-location simulation with vector species and seasonality characteristic of central Tanzania, varying baseline transmission intensity and vector bionomics. The sensitivities to habitat type, anthropophily, indoor feeding, and baseline transmission intensity are explored.

Conclusions: The ability to model a spectrum of local vector species with different ecologies and behaviours allows local customization of packages of interventions and exploration of the effect of proposed new tools.

Figure 1

Effects of climate and weather on vector populations. a) Effect of temperature and humidity on time constant τ_temp for temporary rainfall-driven larval habitat. The habitat decay is faster for warmer and drier weather. b) Temperature effects on duration larval development, with the functional form from [4] and the present Arrhenius formulation. c) Temperature effects on duration of sporogony. The traditional degree-day formula and the present Arrhenius function are plotted, along with Beier's data from [49].

Figure 2

Intermediate outputs which affect vector population or disease transmission dynamics. a) Larval survival of development as a function of temperature and larval mortality. Survival is from successful egg hatch to emergence; survival from oviposition would be significantly lower. b) Adult survival of sporogony as a function of temperature and adult mortality. At lower temperatures, mosquitoes spend longer in each progress queue and the overall effect of a daily mortality is greater. Adult mortality can be artificially increased through interventions such as bed nets, insecticide spraying, and baited traps.

Figure 3

Vector development state space. All eggs of a similar state (species, gender, habitat, Wolbachia type) hatching in a time step begin larval development as a cohort. The only changes to this cohort are the population and the progress, and each time step, mortality reduces the population and progress increments by the Arrhenius temperature-driven rate multiplied by the time step. The progress added can vary depending on the daily temperature and is not constrained to be constant or an integer number of total days, so n1 would be the total development period at the mean temperature of the first time step. When progress through development is complete for a cohort, emergence occurs, and the cohort begins the latency to blood feeding as immature emerged adults. This latency can last for several hours up to several days, at which point the cohort begins the cycle of blood feeding. Adults infected in a time step are removed from their cohort and a new cohort is created for newly infected adults. This new cohort then proceeds through the infected development queue, with mortality reducing the population and temperature-dependent incrementing of progress. Once sporogony is complete, the cohort becomes infectious and remains so until the population is reduced to zero, at which point the cohort is de-allocated.

Figure 4

Calculation of outcomes for each mosquito every time step in the presence of combined interventions. Each choice has a defined probability, and the conditional probabilities can be summed for each overall possible outcome as described in the Appendix. Bed nets can kill or not, and vector feeding time can be adjusted to change the proportion of bites during the period protected by nets. Indoor feeding and resting can be split by adding in an additional decision fork after indoor and outdoor feeds. After a successful indoor feed, a mosquito must make it to an oviposition site alive to lay eggs and survive. Closed loop egg-laying allows interference by interventions to eventually limit population sizes. Individual resolution of the human population ensures that only those infectious mosquitoes that successfully pass through a gauntlet to get to a human successfully can transmit infection.

Figure 5

Baseline population dynamics summed over local populations of An. gambiae ss, An. funestus, and An. arabiensis for different larval habitat multipliers. a) Local weather will drive both the temporary and semi-permanent larval habitats. b) The adult vector population changes as a function of the scaling of the larval habitat carrying capacity, which is driven by local weather. c) The sporozoite rate of mosquito population changes in response to the changing age structure of the vector population over the course of two years. d) Daily EIR combines the adult vector population and the sporozoite rate.

Figure 6

Effects of increasing coverage with perfect IRS. Effects of increasing coverage with perfect IRS (p_{kill, IRSpostfeed} = 1) on a) Adult population c) Sporozoite rate e) EIR. Effects on sporozoite rate and EIR are much more dramatic than on the adult population because of the restructuring of the age distribution of the mosquito population. For most coverage levels, larval habitat remains the limiting factor in the rate of emerging mosquitoes, and number of young, unfed mosquitoes remains similar as IRS coverage increases up to a point. However, the increased feeding mortality results in a decreased life expectancy for mosquitoes, a moderate reduction in total population, but a strong reduction in mosquitoes older than 10 days. b, d, f) Repeated for IRS with (p_{kill, IRSpostfeed} = 0.6). The effects on sporozoite rate and EIR are not as dramatic due to improved mosquito survival. The larval habitat multiplier is set to 3.0 for these simulations.

Figure 7

Effects of combining IRS and ITN. a, b) Probability of Eradication and Estimate Variance for perfect bed nets and IRS, which do not decay, for fully indoor feeding and resting mosquitoes c, d) Bed nets still prevent all nighttime feeds, but only kill 60% of mosquitoes attempting to feed. IRS kills 60% of post-indoor feeding mosquitoes in treated houses. Eradication is no longer possible in many previously possible parameter regions. e, f) Effect of varying indoor feeding and anthropophily of the An. arabiensis population for 90 percent IRS coverage with no decay of insecticide and p_{kill, IRSpostfeed} = 1. The multiplier for larval habitat set to 1.0 for all three sets of simulations, and increasing larval habitat increases the level of coverage required, but not as dramatically as changing the adult mortality. Dark blue regions in a, c, e correspond to parameter regimes in which the estimated probability of local elimination is over 0.9 and dark red less than 0.1. Level sets for mean estimated probability of elimination and for probability estimate variance are labeled.

Figure 8

Larval control and space spraying. Larval control and space spraying introduced to the baseline simulations from Figure 5, with larval habitat multipliers set to 3.0. a, c, e) Larval control on the left reduces adult vector populations and EIR, but does not affect sporozoite rate at these high EIRs as the age structure of the vector population is unaffected. b, d, f) Adult mortality affects all three measures, as it reduces the number of adult vectors, and dramatically changes the age structure so that fewer mosquitoes are old enough to have sporozoites. This creates a compounded effect on EIR.