Constant electric field simulations of the membrane potential illustrated with simple systems

Abstract

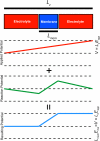
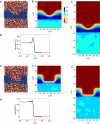
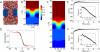
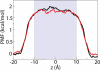
Advances in modern computational methods and technology make it possible to carry out extensive molecular dynamics simulations of complex membrane proteins based on detailed atomic models. The ultimate goal of such detailed simulations is to produce trajectories in which the behavior of the system is as realistic as possible. A critical aspect that requires consideration in the case of biological membrane systems is the existence of a net electric potential difference across the membrane. For meaningful computations, it is important to have well validated methodologies for incorporating the latter in molecular dynamics simulations. A widely used treatment of the membrane potential in molecular dynamics consists of applying an external uniform electric field E perpendicular to the membrane. The field acts on all charged particles throughout the simulated system, and the resulting applied membrane potential V is equal to the applied electric field times the length of the periodic cell in the direction perpendicular to the membrane. A series of test simulations based on simple membrane-slab models are carried out to clarify the consequences of the applied field. These illustrative tests demonstrate that the constant-field method is a simple and valid approach for accounting for the membrane potential in molecular dynamics studies of biomolecular systems. This article is part of a Special Issue entitled: Membrane protein structure and function.

Figure 1

Schematic description of the constant electric field methodology. In the periodic system, the applied constant field is associated with a linear potential, which is combined with the reaction potential from the electrostatic interactions treated via particle mesh Ewald (PME) to generate the resulting total potential. Even though the total electrostatic potential is non-periodic, the reaction potential computed during the simulation (PME), as well as the forces (slopes of curves) from both the applied and total potential are compatible with periodic boundary conditions.

Figure 2

Membrane slab systems. (A) Full simulation system for the simple membrane slab shown as space-filling spheres with the membrane colored in blue; the water in red and white; and Na⁺ and Cl⁻ ions in yellow and cyan, respectively. (B) Time-averaged electrostatic potential for the system in (A). The color gradient to the right indicates the scale for the potential in units of Volts. (C,D) Simulation system and potential identical to those in (A,B) except with the system length doubled and the applied field halved. (E) Potential along the z-axis for the system in A (black) and in C (red).

Figure 3

Alternative simulated membrane geometries. (A) Simulation system for the membrane with a trapezoidal cutout, colored as in Fig. 2A. (B,C) Time-averaged potential for the system in (A) and the same system with its length in z doubled, respectively. (D) Potential along z, centered in x and y, taken from those in B (black) and C (red). (E–H) System and potentials shown as in (A–D) for the membrane with a rectangular cutout.

Figure 4

Membrane with a 20-Å-diameter pore. (A) Simulation system. (B,C) Potentials for the smaller (B) and larger (C) pore-containing systems. (D) Potential along z as in Figs. 2E and 3D,H. (E,F) Current as a function of time for the smaller (E) and larger (F) systems. The inset of each graph shows the displacement charge Q over time.

Figure 5

Potential of mean force (PMF) for a Cl⁻ ion in the 20-Å pore in the absence of an applied field. The black curve represents the system of size L and the red 2L; the extent of the pore is indicated by the shaded blue region. Implicit in the calculation of M(t) is the assumption that it does not depend on the position z of the ion [54]. The relatively flat PMF about z = 0 confirms that there is no contribution from a systematic mean force to the fluctuations.

Figure 6

Effect of size on transport properties. In all panels, the black curve represents the system of length L and the red curve that of length 2L. (A) Memory function, M(t) for the chloride ion in the 20-Å pore. The inset is a close-up of the first 0.5 ps. (B) γ(t) for the two systems. (C,D) Memory function (C) and friction γ (D) for a simple charged particle with no Lennard-Jones interactions restrained in the center of a pure slab.