Finite platelet size could be responsible for platelet margination effect
- PMID: 22004736
- PMCID: PMC3192962
- DOI: 10.1016/j.bpj.2011.08.031
Finite platelet size could be responsible for platelet margination effect
Abstract
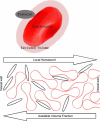
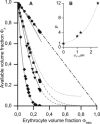
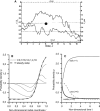
Blood flows through vessels as a segregated suspension. Erythrocytes distribute closer to the vessel axis, whereas platelets accumulate near vessel walls. Directed platelet migration to the vessel walls promotes their hemostatic function. The mechanisms underlying this migration remain poorly understood, although various hypotheses have been proposed to explain this phenomenon (e.g., the available volume model and the drift-flux model). To study this issue, we constructed a mathematical model that predicts the platelet distribution profile across the flow in the presence of erythrocytes. This model considers platelet and erythrocyte dimensions and assumes an even platelet distribution between erythrocytes. The model predictions agree with available experimental data for near-wall layer margination using platelets and platelet-modeling particles and the lateral migration rate for these particles. Our analysis shows that the strong expulsion of the platelets from the core to the periphery of the blood vessel may mainly arise from the finite size of the platelets, which impedes their positioning in between the densely packed erythrocytes in the core. This result provides what we believe is a new insight into the rheological control of platelet hemostasis by erythrocytes.
Copyright © 2011 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures

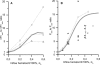

Similar articles
-
The influence of red blood cell deformability on hematocrit profiles and platelet margination.PLoS Comput Biol. 2020 Mar 12;16(3):e1007716. doi: 10.1371/journal.pcbi.1007716. eCollection 2020 Mar. PLoS Comput Biol. 2020. PMID: 32163405 Free PMC article.
-
Near-wall excess of platelets induced by lateral migration of erythrocytes in flowing blood.Am J Physiol. 1993 Apr;264(4 Pt 2):H1239-44. doi: 10.1152/ajpheart.1993.264.4.H1239. Am J Physiol. 1993. PMID: 8476101
-
Quantifying Platelet Margination in Diabetic Blood Flow.Biophys J. 2018 Oct 2;115(7):1371-1382. doi: 10.1016/j.bpj.2018.08.031. Epub 2018 Aug 30. Biophys J. 2018. PMID: 30224049 Free PMC article.
-
Platelet-vessel wall interactions in the microcirculation.Microcirculation. 2005 Apr-May;12(3):275-85. doi: 10.1080/10739680590925691. Microcirculation. 2005. PMID: 15814436 Review.
-
Thromboregulation: multicellular modulation of platelet reactivity in hemostasis and thrombosis.FASEB J. 1993 Apr 1;7(6):516-22. doi: 10.1096/fasebj.7.6.8472890. FASEB J. 1993. PMID: 8472890 Review.
Cited by
-
Skin Acute Wound Healing: A Comprehensive Review.Int J Inflam. 2019 Jun 2;2019:3706315. doi: 10.1155/2019/3706315. eCollection 2019. Int J Inflam. 2019. PMID: 31275545 Free PMC article. Review.
-
Platelet "first responders" in wound response, cancer, and metastasis.Cancer Metastasis Rev. 2017 Jun;36(2):199-213. doi: 10.1007/s10555-017-9682-0. Cancer Metastasis Rev. 2017. PMID: 28730545 Free PMC article. Review.
-
Red blood cell distribution width is associated with increased interactions of blood cells with vascular wall.Sci Rep. 2022 Aug 11;12(1):13676. doi: 10.1038/s41598-022-17847-z. Sci Rep. 2022. PMID: 35953533 Free PMC article.
-
Platelets involved tumor cell EMT during circulation: communications and interventions.Cell Commun Signal. 2022 Jun 3;20(1):82. doi: 10.1186/s12964-022-00887-3. Cell Commun Signal. 2022. PMID: 35659308 Free PMC article. Review.
-
Biomaterials and Advanced Technologies for Hemostatic Management of Bleeding.Adv Mater. 2018 Jan;30(4):10.1002/adma.201700859. doi: 10.1002/adma.201700859. Epub 2017 Nov 22. Adv Mater. 2018. PMID: 29164804 Free PMC article. Review.
References
-
- Ruggeri Z.M., Mendolicchio G.L. Adhesion mechanisms in platelet function. Circ. Res. 2007;100:1673–1685. - PubMed
-
- Goldsmith H.L. Red cell motions and wall interactions in tube flow. Fed. Proc. 1971;30:1578–1590. - PubMed
-
- Goldsmith H.L., Skalak R. Hemodynamics. Annu. Rev. Fluid Mech. 1975;7:213–247.
-
- Goldsmith H.L., Marlow J.C. Flow behavior of erythrocytes. II. Particle motions in concentrated suspensions of ghost cells. J. Colloid Interface Sci. 1979;71:383–407.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

