The influence of complex white matter architecture on the mean diffusivity in diffusion tensor MRI of the human brain

Abstract

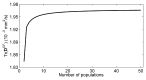
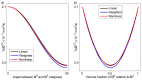
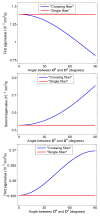
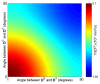
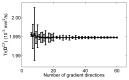
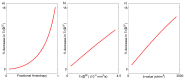
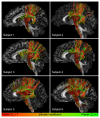
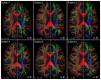
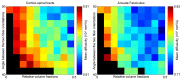
In diffusion tensor magnetic resonance imaging (DT-MRI), limitations concerning complex fiber architecture (when an image voxel contains fiber populations with more than one dominant orientation) are well-known. Fractional anisotropy (FA) values are lower in such areas because of a lower directionality of diffusion on the voxel-scale, which makes the interpretation of FA less straightforward. Moreover, the interpretation of the axial and radial diffusivities is far from trivial when there is more than one dominant fiber orientation within a voxel. In this work, using (i) theoretical considerations, (ii) simulations, and (iii) experimental data, it is demonstrated that the mean diffusivity (or the trace of the diffusion tensor) is lower in complex white matter configurations, compared with tissue where there is a single dominant fiber orientation within the voxel. We show that the magnitude of this reduction depends on various factors, including configurational and microstructural properties (e.g., the relative contributions of different fiber populations) and acquisition settings (e.g., the b-value). These results increase our understanding of the quantitative metrics obtained from DT-MRI and, in particular, the effect of the microstructural architecture on the mean diffusivity. More importantly, they reinforce the growing awareness that differences in DT-MRI metrics need to be interpreted cautiously.

Figure 1

The calculated trace in a “crossing fibers” voxel, Tr(D^CF), is shown for a crossing with a varying number of orientations in a plane. Such a configuration could be considered analogous to fibers fanning out in a voxel, as for instance can be found in the cortico-spinal tracts. Compared with the trace in a voxel with one fiber orientation (Tr(D^SF) = 2.1 × 10⁻³ mm²/s), the Tr(D^CF) is strongly reduced for two orientations. With more orientations, Tr(D^CF) gradually increases, stabilizing in the range of 30–50 fiber orientations.

Figure 2

(a) Increasing the angle of intersection between two fiber populations (D^A and D^B) up to 90° decreases the trace in a “crossing fibers” configurations, Tr(D^CF). Performing this simulation with three types of tensor estimation shows that the choice of tensor estimation also affects the trace (linear least squares estimation is illustrated in black, weighted least squares in blue, nonlinear least squares in red). (b) The volume fractions of the two populations in one voxel also modulates Tr(D^CF). As in (a), the type of tensor estimation also affects the trace in (b).

Figure 3

Diffusivity profiles of the first, second, and third eigenvalues depending on the angle of intersection between the two fiber populations (D^A and D^B). The first eigenvalue is smaller in “crossing fibers” configurations than in “single fiber” configurations, whereas the second and third eigenvalues are larger.

Figure 4

When three fiber populations intersect, the trace (Tr(DC^F)) is affected by the angle of both the second (D^B) and third (DC) population with respect to the first population (D^A).

Figure 5

Variation in the estimated trace in a “crossing fibers” configuration, Tr(D^CF), depending on the number of unique sampling directions for two populations crossing at 90°. The average Tr(DC^F) and standard deviation (error bars) have been calculated from over 4000 different orientations. Tr(DC^F) is lower than the trace in single fiber voxels (Tr(D^SF) = 2.1×10⁻³ mm²/s) for all number of gradient directions.

Figure 6

The effect of simulation parameters (a: fractional anisotropy; b: trace of a “single fiber” population (Tr(D^SF)); c: b-value) on the relative decrease in trace in a “crossing fibers” configuration, Tr(D^CF), with two orthogonally oriented fiber populations (with equal volume fractions).

Figure 7

Sagittal views of a fractional anisotropy map with the cortico-spinal tracts and arcuate fasciculus for all six subjects. Tracts are color-encoded by the linear and planar diffusion coefficients (C_L and C_P, respectively), where red indicates linear diffusion and green indicates planar diffusion.

Figure 8

For all subjects, axial slices at the level of the corpus callosum are shown with geometric and direction-encoded color coding. In the geometric image, red and green voxels correspond with the linear (C_L) and planar (C_P) diffusion coefficients, respectively. Regions of linear and planar diffusion can clearly be differentiated throughout the white matter.

Figure 9

The mean diffusivity (trace/3) is affected by configurational properties of the white matter. The mean diffusivity decreases as the angle between two fiber populations increases, and the relative volume fractions become more equal. The angles between two fiber populations, as well as the relative volume fractions of these populations, have been determined from constrained spherical deconvolution. The black regions are configurations that were not present.