Optimal control of the lost to follow up in a tuberculosis model
- PMID: 22007263
- PMCID: PMC3191742
- DOI: 10.1155/2011/398476
Optimal control of the lost to follow up in a tuberculosis model
Abstract
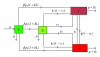
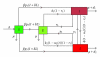
This paper deals with the problem of optimal control for the transmission dynamics of tuberculosis (TB). A TB model that considers the existence of a new class (mainly in the African context) is considered: the lost to follow up individuals. Based on the model formulated and studied in the work of Plaire Tchinda Mouofo, (2009), the TB control is formulated and solved as an optimal control theory problem using the Pontryagin's maximum principle (Pontryagin et al., 1992). This control strategy indicates how the control of the lost to follow up class can considerably influence the basic reproduction ratio so as to reduce the number of lost to follow up. Numerical results show the performance of the optimization strategy.
Figures





Similar articles
-
Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control.Theor Biol Med Model. 2020 May 4;17(1):6. doi: 10.1186/s12976-020-00124-9. Theor Biol Med Model. 2020. PMID: 32362279 Free PMC article.
-
Impact of media coverage on the transmission dynamics of TB with vaccines and treatment.PLoS One. 2025 Jan 28;20(1):e0314324. doi: 10.1371/journal.pone.0314324. eCollection 2025. PLoS One. 2025. PMID: 39874254 Free PMC article.
-
Dynamics and optimal control of tuberculosis model with the combined effects of vaccination, treatment and contaminated environments.Math Biosci Eng. 2024 Mar 7;21(4):5308-5334. doi: 10.3934/mbe.2024234. Math Biosci Eng. 2024. PMID: 38872537
-
Dynamics and control of the global tuberculosis epidemic.Curr Opin Pulm Med. 2000 May;6(3):174-9. doi: 10.1097/00063198-200005000-00002. Curr Opin Pulm Med. 2000. PMID: 10782699 Review.
-
[Organization of tuberculosis control in France in 2011].Rev Prat. 2012 Apr;62(4):507-9. Rev Prat. 2012. PMID: 22641892 Review. French. No abstract available.
Cited by
-
Optimal control for an age-structured model for the transmission of hepatitis B.J Math Biol. 2016 Aug;73(2):305-33. doi: 10.1007/s00285-015-0952-6. Epub 2015 Dec 16. J Math Biol. 2016. PMID: 26676356
-
Quantifying TB transmission: a systematic review of reproduction number and serial interval estimates for tuberculosis.Epidemiol Infect. 2018 Sep;146(12):1478-1494. doi: 10.1017/S0950268818001760. Epub 2018 Jul 4. Epidemiol Infect. 2018. PMID: 29970199 Free PMC article.
References
-
- Bercion R, Kuaban C. Resistance of Mycobacterium tuberculosis complex to the main antituberculosis drugs in Yaounde-Cameroon. Bulletin de la Societe de Pathologie Exotique. 1998;91(3):199–202. - PubMed
-
- Global Tuberculosis Control: Surveillance, Planning, Financing. Geneva, Switzerland: World Health Organization; 2005.
-
- Feng Z, Castillo-Chavez C. Mathematical Models for the Disease Dynamics of Tubeculosis. River Edge, NJ, USA: World Scientific Publishing; 1998.
-
- Blower SM, Small PM, Hopewell PC. Control strategies for tuberculosis epidemics: New models for old problems. Science. 1996;273(5274):497–500. - PubMed
-
- Bowong S, Emvudu Y, Moualeu DP, Tewa JJ. Mathematical properies of a tuberculosis model with two differential infectivity and N latent classes. Journal of Nonlinear Systems and Applications. 2010:13–26.
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

