Individual subject classification for Alzheimer's disease based on incremental learning using a spatial frequency representation of cortical thickness data
- PMID: 22008371
- PMCID: PMC5849264
- DOI: 10.1016/j.neuroimage.2011.09.085
Individual subject classification for Alzheimer's disease based on incremental learning using a spatial frequency representation of cortical thickness data
Abstract
Patterns of brain atrophy measured by magnetic resonance structural imaging have been utilized as significant biomarkers for diagnosis of Alzheimer's disease (AD). However, brain atrophy is variable across patients and is non-specific for AD in general. Thus, automatic methods for AD classification require a large number of structural data due to complex and variable patterns of brain atrophy. In this paper, we propose an incremental method for AD classification using cortical thickness data. We represent the cortical thickness data of a subject in terms of their spatial frequency components, employing the manifold harmonic transform. The basis functions for this transform are obtained from the eigenfunctions of the Laplace-Beltrami operator, which are dependent only on the geometry of a cortical surface but not on the cortical thickness defined on it. This facilitates individual subject classification based on incremental learning. In general, methods based on region-wise features poorly reflect the detailed spatial variation of cortical thickness, and those based on vertex-wise features are sensitive to noise. Adopting a vertex-wise cortical thickness representation, our method can still achieve robustness to noise by filtering out high frequency components of the cortical thickness data while reflecting their spatial variation. This compromise leads to high accuracy in AD classification. We utilized MR volumes provided by Alzheimer's Disease Neuroimaging Initiative (ADNI) to validate the performance of the method. Our method discriminated AD patients from Healthy Control (HC) subjects with 82% sensitivity and 93% specificity. It also discriminated Mild Cognitive Impairment (MCI) patients, who converted to AD within 18 months, from non-converted MCI subjects with 63% sensitivity and 76% specificity. Moreover, it showed that the entorhinal cortex was the most discriminative region for classification, which is consistent with previous pathological findings. In comparison with other classification methods, our method demonstrated high classification performance in both categories, which supports the discriminative power of our method in both AD diagnosis and AD prediction.
Copyright © 2011 Elsevier Inc. All rights reserved.
Figures


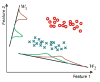
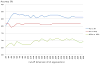

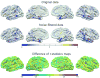

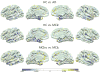

References
-
- Balakrishnama S, Ganapathiraju A. Linear discriminant analysis - a brief tutorial [online] 1998 Available: http://www.music.mcgill.ca/ich/classes/mumt61105/classifiers/ldatheory.pdf.
-
- Belhumeur PN, Hespanha JP, Kriegman DJ. Eigenfaces vs. fisherfaces: Recognition using class specific linear projection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19:711–720.
-
- Bylesjø M, Rantalainen M, Cloarec O, Nicholson JK, Holmes E, Tryg J. Opls discriminant analysis: combining the strengths of pls-da and simca classification. Journal of Chemometrics. 2006;20 (8–10):341–351.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

