Optimization of nonlinear dose- and concentration-response models utilizing evolutionary computation

Abstract

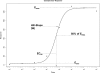
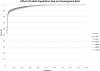
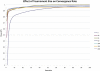
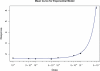
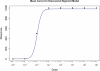
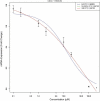
An essential part of toxicity and chemical screening is assessing the concentrated related effects of a test article. Most often this concentration-response is a nonlinear, necessitating sophisticated regression methodologies. The parameters derived from curve fitting are essential in determining a test article's potency (EC(50)) and efficacy (E(max)) and variations in model fit may lead to different conclusions about an article's performance and safety. Previous approaches have leveraged advanced statistical and mathematical techniques to implement nonlinear least squares (NLS) for obtaining the parameters defining such a curve. These approaches, while mathematically rigorous, suffer from initial value sensitivity, computational intensity, and rely on complex and intricate computational and numerical techniques. However if there is a known mathematical model that can reliably predict the data, then nonlinear regression may be equally viewed as parameter optimization. In this context, one may utilize proven techniques from machine learning, such as evolutionary algorithms, which are robust, powerful, and require far less computational framework to optimize the defining parameters. In the current study we present a new method that uses such techniques, Evolutionary Algorithm Dose Response Modeling (EADRM), and demonstrate its effectiveness compared to more conventional methods on both real and simulated data.

Keywords: Evolutionary Algorithm; Hill-Slope Model; Nonlinear Regression; Parameter Estimation.

FIGURE 1:

Example Nonlinear Dose-Response

FIGURE 2:

Evolutionary Algorithm Overview

FIGURE 3:

Effect of Initial Population Size on Convergence Rate

FIGURE 4:

Effect of Equilibrium Population Size on Convergence Rate

FIGURE 5:

Effect of Initial Tournament Size on Convergence Rate

FIGURE 6:

Execution Time vs. Initial Population Size

FIGURE 7:

Execution Time vs. Equilibrium Population Size

FIGURE 8:

Execution Time vs. Equilibrium Population Size

FIGURE 9:

Resulting Fit from Exponential Model

FIGURE 10:

Result from Simulating both Exponential and Hillslope individuals on Hillslope Data

FIGURE 11:

Concentration-Response for CYP3A4/RIF

FIGURE 12:

HMGCS2 Suppression by CDCA. Note that the green and red lines overlap, and are not distinguishable visually.