A computational study of how orientation bias in the lateral geniculate nucleus can give rise to orientation selectivity in primary visual cortex
- PMID: 22013414
- PMCID: PMC3190185
- DOI: 10.3389/fnsys.2011.00081
A computational study of how orientation bias in the lateral geniculate nucleus can give rise to orientation selectivity in primary visual cortex
Abstract
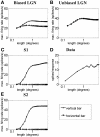
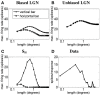
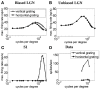
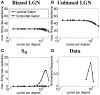
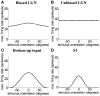
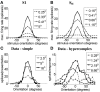
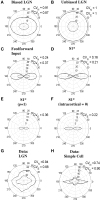
Controversy remains about how orientation selectivity emerges in simple cells of the mammalian primary visual cortex. In this paper, we present a computational model of how the orientation-biased responses of cells in lateral geniculate nucleus (LGN) can contribute to the orientation selectivity in simple cells in cats. We propose that simple cells are excited by lateral geniculate fields with an orientation-bias and disynaptically inhibited by unoriented lateral geniculate fields (or biased fields pooled across orientations), both at approximately the same retinotopic co-ordinates. This interaction, combined with recurrent cortical excitation and inhibition, helps to create the sharp orientation tuning seen in simple cell responses. Along with describing orientation selectivity, the model also accounts for the spatial frequency and length-response functions in simple cells, in normal conditions as well as under the influence of the GABA(A) antagonist, bicuculline. In addition, the model captures the response properties of LGN and simple cells to simultaneous visual stimulation and electrical stimulation of the LGN. We show that the sharp selectivity for stimulus orientation seen in primary visual cortical cells can be achieved without the excitatory convergence of the LGN input cells with receptive fields along a line in visual space, which has been a core assumption in classical models of visual cortex. We have also simulated how the full range of orientations seen in the cortex can emerge from the activity among broadly tuned channels tuned to a limited number of optimum orientations, just as in the classical case of coding for color in trichromatic primates.
Keywords: length–response function; orientation tuning; simple cells; spatial frequency; striate cortex.
Figures

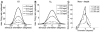


Similar articles
-
Orientation tuning of surround suppression in lateral geniculate nucleus and primary visual cortex of cat.Neuroscience. 2007 Nov 23;149(4):962-75. doi: 10.1016/j.neuroscience.2007.08.001. Epub 2007 Aug 9. Neuroscience. 2007. PMID: 17945429
-
Role of feedforward geniculate inputs in the generation of orientation selectivity in the cat's primary visual cortex.J Physiol. 2011 May 1;589(Pt 9):2349-61. doi: 10.1113/jphysiol.2010.202317. Epub 2011 Mar 14. J Physiol. 2011. PMID: 21486788 Free PMC article.
-
Relationship between the Dynamics of Orientation Tuning and Spatiotemporal Receptive Field Structures of Cat LGN Neurons.Neuroscience. 2018 May 1;377:26-39. doi: 10.1016/j.neuroscience.2018.02.024. Epub 2018 Feb 23. Neuroscience. 2018. PMID: 29481999
-
A spherical model for orientation and spatial-frequency tuning in a cortical hypercolumn.Philos Trans R Soc Lond B Biol Sci. 2003 Oct 29;358(1438):1643-67. doi: 10.1098/rstb.2002.1109. Philos Trans R Soc Lond B Biol Sci. 2003. PMID: 14561324 Free PMC article. Review.
-
Origins of feature selectivities and maps in the mammalian primary visual cortex.Trends Neurosci. 2015 Aug;38(8):475-85. doi: 10.1016/j.tins.2015.06.003. Epub 2015 Jul 22. Trends Neurosci. 2015. PMID: 26209463 Review.
Cited by
-
Emergence of orientation selectivity in the Mammalian visual pathway.J Neurosci. 2013 Jun 26;33(26):10616-24. doi: 10.1523/JNEUROSCI.0404-13.2013. J Neurosci. 2013. PMID: 23804085 Free PMC article.
-
Subcortical orientation biases explain orientation selectivity of visual cortical cells.Physiol Rep. 2015 Apr;3(4):e12374. doi: 10.14814/phy2.12374. Physiol Rep. 2015. PMID: 25855249 Free PMC article.
-
Cortical Surround Interactions and Perceptual Salience via Natural Scene Statistics.PLoS Comput Biol. 2012;8(3):e1002405. doi: 10.1371/journal.pcbi.1002405. Epub 2012 Mar 1. PLoS Comput Biol. 2012. PMID: 22396635 Free PMC article.
-
Thalamus provides layer 4 of primary visual cortex with orientation- and direction-tuned inputs.Nat Neurosci. 2016 Feb;19(2):308-15. doi: 10.1038/nn.4196. Epub 2015 Dec 21. Nat Neurosci. 2016. PMID: 26691829 Free PMC article.
-
Leveraging neural plasticity for the treatment of amblyopia.Surv Ophthalmol. 2024 Sep-Oct;69(5):818-832. doi: 10.1016/j.survophthal.2024.04.006. Epub 2024 May 18. Surv Ophthalmol. 2024. PMID: 38763223 Review.
References
-
- Allison J. D., Smith K. R., Bonds A. B. (2001). Temporal-frequency tuning of cross-orientation suppression in the cat striate cortex. Vis. Neurosci. 18, 941–948 - PubMed
-
- Bloomfield S. A., Sherman S. M. (1988). Postsynaptic potentials recorded in neurons of the cat’s lateral geniculate nucleus following electrical stimulation of the optic chiasm. J. Neurophysiol. 60, 1924–1945 - PubMed
LinkOut - more resources
Full Text Sources
Miscellaneous

