Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Comment
. 2011 Dec 1;174(11):1223-7; discussion pg 1228-9.
doi: 10.1093/aje/kwr352. Epub 2011 Oct 27.

Invited commentary: understanding bias amplification

Judea Pearl  1
Affiliations
Comment

Invited commentary: understanding bias amplification

Judea Pearl. Am J Epidemiol. .

Abstract

In choosing covariates for adjustment or inclusion in propensity score analysis, researchers must weigh the benefit of reducing confounding bias carried by those covariates against the risk of amplifying residual bias carried by unmeasured confounders. The latter is characteristic of covariates that act like instrumental variables-that is, variables that are more strongly associated with the exposure than with the outcome. In this issue of the Journal (Am J Epidemiol. 2011;174(11):1213-1222), Myers et al. compare the bias amplification of a near-instrumental variable with its bias-reducing potential and suggest that, in practice, the latter outweighs the former. The author of this commentary sheds broader light on this comparison by considering the cumulative effects of conditioning on multiple covariates and showing that bias amplification may build up at a faster rate than bias reduction. The author further derives a partial order on sets of covariates which reveals preference for conditioning on outcome-related, rather than exposure-related, confounders.

PubMed Disclaimer

Figures

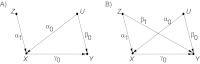
Figure 1.
Figure 1.
A) A linear model with instrumental variable Z and confounder U. B) A near-instrumental variable Z that is also a confounder.
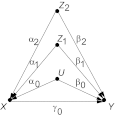
Figure 2.
Figure 2.
A linear model with multiple covariates (Z1 and Z2) and an unobserved confounder U.
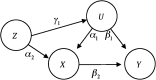
Figure 3.
Figure 3.
The model used by Myers et al. for studying near-instrumental variables. The parameter γ1 contributes to confounding as well as to bias amplification.
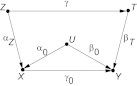
Figure 4.
Figure 4.
Adjustment for an output-related covariate (T) is preferred to adjustment for a treatment-related covariate (Z) or both (Z, T). The former covariate has a lower bias-amplification potential than the latter two when U is unobserved.
See this image and copyright information in PMC

Comment on

References

    1. Bhattacharya J, Vogt W. Do Instrumental Variables Belong in Propensity Scores? (NBER Technical Working Paper no. 343). Cambridge, MA: National Bureau of Economic Research; 2007.
    1. Wooldridge J. Should instrumental variables be used as matching variables? East Lansing, MI: Michigan State University; 2009. ( https://www.msu.edu/∼ec/faculty/wooldridge/current%20research/treat1r6.pdf). (Accessed July 2010)
    1. Pearl J. Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence (UAI 2010) Corvallis, OR: Association for Uncertainty in Artificial Intelligence; 2010. On a class of bias-amplifying variables that endanger effect estimates; pp. 425–432. ( http://ftp.cs.ucla.edu/pub/stat_ser/r356.pdf). (Accessed September 2011)
    1. Myers JA, Rassen JA, Gagne JJ, et al. Effects of adjusting for instrumental variables on bias and precision of effect estimates. Am J Epidemiol. 2011;174(11):1213–1222. - PMC - PubMed
    1. White H, Lu X. Causal diagrams for treatment effect estimation with application to efficient covariate selection. Rev Econ Stat. In press

Publication types